Sujet et corrigé de l'exercice 1 du bac ES de maths d'avril 2016 à Pondichéry
Cacher les corrigés
1. Soit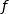 
la fonction définie sur l'intervalle 
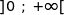par 
.
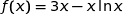On admet que 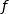est dérivable sur l'intervalle 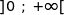et on désigne par 
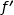sa fonction dérivée.
Pour tout nombre réel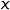 
de l'intervalle 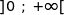on a :
(a)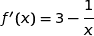 
(b)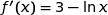 
(c)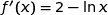 
La fonction 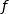est définie et dérivable sur l'intervalle .
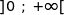On peut écrire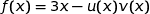 
avec :
; 
; 
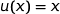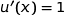
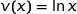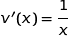
Par suite :
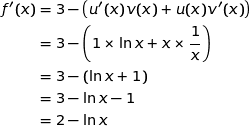
La bonne réponse est la réponse (c).
2. On considère la suite géométrique de premier terme 1 et de raison 2.
La somme des 13 premiers termes de cette suite vaut :
(a) 4095
(b) 8191
(c)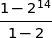 
Attention les 13 premiers termes de la suite c'est :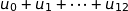 
où :
;
;
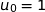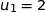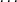
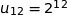
En utilisant la formule vue en cours nous avons :
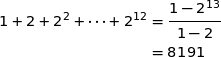
La bonne réponse est la réponse (b).
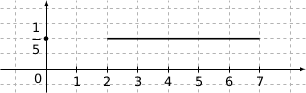
3. Une variable aléatoire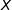 
suit une loi uniforme sur l'intervalle 
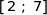dont la fonction de densité est représentée ci-dessous.
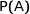désigne la probabilité de l'événement A et 
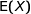l'espérance de la variable aléatoire .
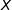(a)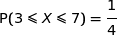 
(b)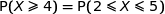 
(c)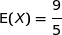 
On peut vérifier les propositions une à une :
Pour la loi uniforme sur :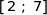
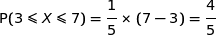
Donc la proposition (a) est fausse.
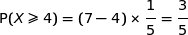
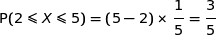
Donc la proposition (b) est juste.
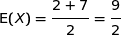.Donc la proposition (c) est fausse.
La bonne réponse est la réponse (b).
4. On réalise un sondage sur un échantillon de 
personnes (, entier naturel non nul).
Parmi les tailles de l'échantillon proposées ci-dessous, quelle est celle qui permet d'obtenir un intervalle de confiance au niveau de confiance 0,95 avec une amplitude de 0,02 ?
(a)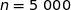 
(b)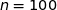 
(c)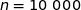 
On sait que l'amplitude de l'intervalle de confiance considéré est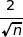 
, du coup on résout :
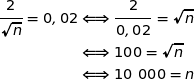
La bonne réponse est la réponse (c).
