Corrigé de l'exercice 4 du bac ES de maths de juin 2012 en Asie
Cacher les corrigés
On s'intéresse à une entreprise de détergents industriels. Elle produit chaque jour une quantité
en tonnes comprise entre 0 et 20. On rappelle que :
- le coût marginal
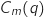est la variation du coût obtenue par la production et la vente d'une tonne supplémentaire de détergent sachant qu'on en a déjà vendu une quantité de tonnes.
- le bénéfice marginal
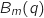est la différence entre le prix unitaire et le coût marginal .
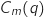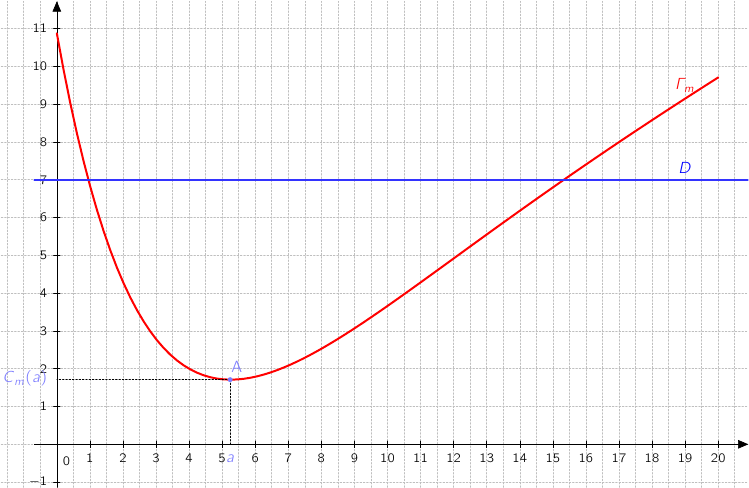
Partie A : Aspect graphique
Dans le repère suivant, on donne :- la courbe représentative
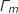de la fonction 
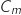correspondant au coût marginal en milliers d'euros ;
- la courbe représentative
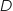de la fonction 
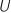correspondant au prix de vente unitaire en milliers d'euros ;
- le point A
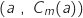, sommet de la courbe .
.
.
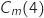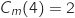2. Déterminer graphiquement
.
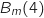Donner une interprétation de ce résultat dans le contexte de l'entreprise.
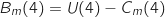
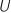est la fonction constante égale à 7 représentée par la droite 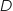, donc on a :
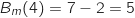
On regarde les abscisses des points d'intersection de 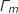et .
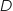On en déduit que le bénéfice marginal est nul pour environ 1 tonne et pour environ 15,5 tonnes.
4. En déduire un encadrement de la quantité à produire, en tonnes, pour obtenir un bénéfice marginal positif.
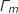et .
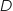On en déduit que le bénéfice marginal est nul pour environ 1 tonne et pour environ 15,5 tonnes.
Le bénéfice marginal est positif lorsque sur le graphique 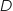est située au dessus de 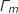soit pour une quantité telle que :
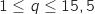
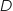est située au dessus de 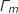soit pour une quantité telle que :
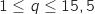
Partie B : Aspect algébrique
Dans cette partie, le coût marginal est donné par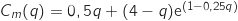
pour appartenant à l'intervalle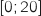 
et le prix de vente unitaire est donné par 
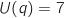pour appartenant à l'intervalle 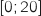. On admet que la fonction 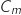est dérivable sur l'intervalle 
.
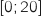Le tableau de variation de la fonction 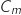est donné ci-dessous. On admet que le nombre réel 
est compris entre 5 et 6.
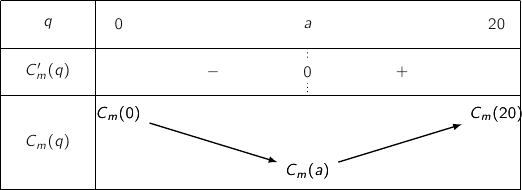
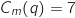admet une unique solution 
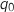dans l'intervalle 
.
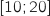Comme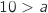 
, sur l'intervalle 
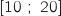la fonction 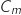est continue et strictement croissante avec :
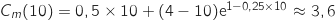
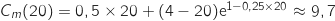Donc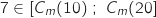 
et d'après le théorème des valeurs intermédiaires il existe un unique 
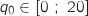tel que
.
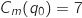b. A l'aide de votre calculatrice, donner un arrondi de 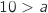, sur l'intervalle 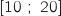la fonction 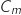est continue et strictement croissante avec :
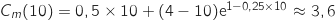
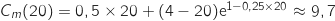Donc 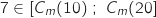et d'après le théorème des valeurs intermédiaires il existe un unique 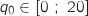tel que
.
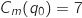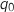au dixième.
Par balayage on trouve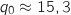 
.
c. Donner, en justifiant, la valeur de .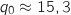
.
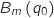Ce résultat est-il cohérent avec la question 3 de la partie A ?
.
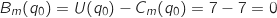Dans la question 3 de la partie A, on avait évalué un bénéfice marginal nul pour 15,5 tonnes produites, donc la valeur 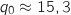est cohérente.
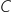, définie sur l'intervalle 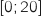par :
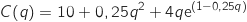
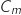. Cette fonction 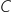est la fonction coût total.
On dérive la fonction :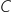
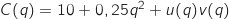avec :
; 
; 
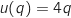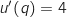
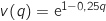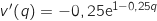(on n'oublie pas le 
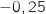en facteur en dérivant la composée).
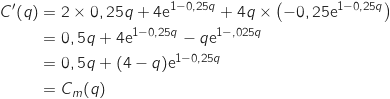Donc 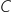est bien une primitive de .
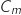3. Déterminer le bénéfice total obtenu pour la fabrication et la vente de 15,3 tonnes de détergent.
:
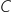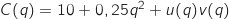avec :
;
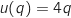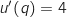
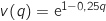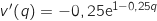; (on n'oublie pas le 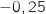en facteur en dérivant la composée).
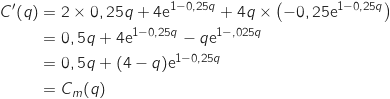Donc 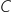est bien une primitive de .
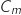Le bénéfice total est donné par :
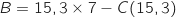avec 
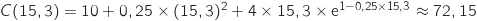Donc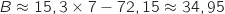 
, c'est à dire environ 34950 €.
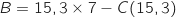avec
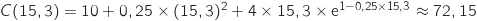Donc 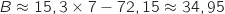, c'est à dire environ 34950 €.
