Corrigé de l'exercice 1 du bac ES de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions posées, une seule des trois réponses est exacte. Pour chaque question, indiquer par a), b) ou c) l'unique bonne réponse. Aucune justification n'est demandée. Une réponse exacte rapporte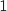
point. Une réponse fausse ou l'absence de réponse ne rapporte ni n'enlève aucun point.
On considère la fonction 
définie et dérivable sur l'intervalle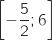 
.
La courbe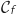 
tracée ci-dessous, représente la fonction dans le plan muni d'un repère orthonormé.
Le point A a pour coordonnées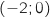 
, le point B a pour coordonnées 
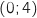, le point C a pour coordonnées 
,
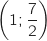le point D a pour coordonnées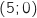 
et le point E a pour coordonnées 
.
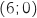On précise que la droite (CE) est tangente à la courbe
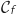au point C et que la courbe admet au point B une tangente horizontale.
et 
les fonctions définies respectivement par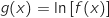 
et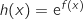 
.
1. La fonction est définie sur l'intervalle :
Pour pouvoir calculer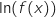 
on doit avoir 
.
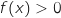Cela se produit sur l'intervalle 
.
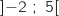La bonne réponse est la réponse a).
2. Le nombre 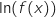on doit avoir .
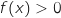Cela se produit sur l'intervalle .
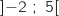La bonne réponse est la réponse a).
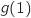est égal à :
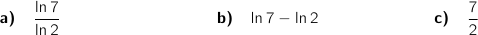
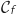passe par 
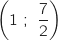donc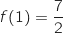 
et on a :
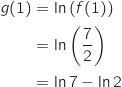La bonne réponse est la réponse b).
3. On note
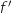la fonction dérivée de , le nombre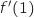 
est égal à :
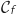est égal au coefficient directeur de la tangente à au point C. Cette tangente est la droite (CE).
Le coefficient directeur est :
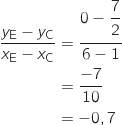La bonne réponse est la réponse c).
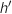la fonction dérivée de 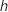, le nombre 
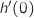est égal à :
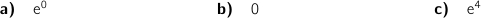
Au point d'abscisse 0, la tangente à 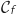est horizontale donc 
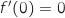et on a :
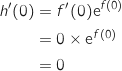La bonne réponse est la réponse b).
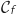est horizontale donc 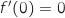et on a :
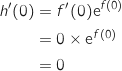La bonne réponse est la réponse b).
