Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2015 en Asie
Cacher les corrigés
Les trois parties de cet exercice sont indépendantes. Les probabilités seront arrondies au millième.
Partie A
Un concurrent participe à un concours de tir à l'arc, sur une cible circulaire. A chaque tir, la probabilité qu'il atteigne la cible est égale à 0,8.
1. Le concurrent tire quatre flèches. On considère que les tirs sont indépendants. Déterminer la probabilité qu'il atteigne au moins trois fois la cible.
Nous avons à faire à la répétition de 4 expériences de Bernoulli identiques et indépendantes dont la probabilité du succès est 0,8.
La variable aléatoire qui compte le nombre de flèches qui atteignent la cible suit la loi binomiale de paramètres et .
2. Combien de flèches le concurrent doit-il prévoir pour atteindre en moyenne la cible douze fois ?
On cherche pour que l'espérance de la loi binomiale soit égale à 12 soit :
Donc le concurrent doit prévoir 15 flèches pour atteindre en moyenne la cible douze fois.
Partie B
Entre deux phases du concours, pour se perfectionner, le concurrent travaille sa précision latérale sur une autre cible d'entraînement, représentée ci-dessous.
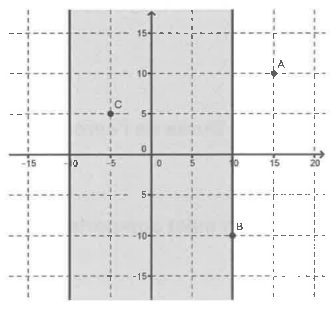
Pour cela, il tire des flèches pour essayer d'atteindre une bande verticale, de largeur 20 cm (en grisé sur la figure), le plus près possible de la ligne verticale centrale.
On munit le plan contenant la bande verticale d'un repère : la ligne centrale visée est l'axe des ordonnées.
On note la variable aléatoire qui, à toute flèche tirée atteignant ce plan, associe l'abscisse de son point d'impact.
Ainsi, par exemple :
si la flèche atteint le point A, le tireur a raté la bande, et prend la valeur 15;
si elle atteint le point B, l'impact est à la limite de la bande, et prend la valeur 10;
si elle atteint le point C, l'impact est dans la bande et prend la valeur .
On suppose que la variable aléatoire suit une loi normale d'espérance 0 et d'écart-type 10.
1. Lorsque la flèche atteint le plan, déterminer la probabilité que son point d'impact soit situé hors de la bande grisée.
Il s'agit de calculer :
2. Comment modifier les bords de la bande grisée pour faire en sorte que, lorsque la flèche atteint le plan, son point d'impact soit situé à l'intérieur de la bande avec une probabilité égale à 0,6 ?
On cherche tel que :
Un petit dessin pour mieux voir ce qu'il se passe :
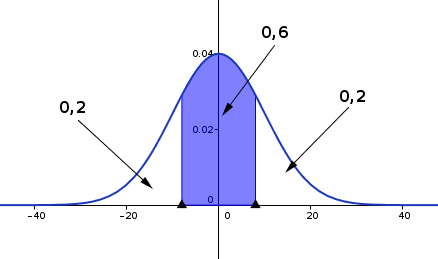
Avec la fonction « Inverse Normale » de la calculatrice, on trouve tel que ce qui donne .
(Sur CASIO : régler tail à left).
Donc il faut placer les bandes aux abscisses : et .
Partie C
La durée de vie (exprimée en heures) du panneau électrique affichant le score des concurrents est une variable aléatoire qui suit la loi exponentielle de paramètre (exprimé en h).
1. Quelle est la probabilité que le panneau fonctionne au moins pendant 2 000 heures ?
On calcule :
2. Restitution organisée des connaissances
Dans cette question, désigne un réel strictement positif.
On rappelle que l'espérance mathématique de la variable aléatoire suivant une loi exponentielle de paramètre , est définie par : E.
a. On considère la fonction , définie pour tout réel par : .
Démontrer que la fonction est une primitive sur de la fonction définie pour tout réel par : .
La fonction est dérivable sur et on a :
où :
;
;
b. En déduire que l'espérance mathématique de la variable aléatoire est égale à .
Quelle est l'espérance de durée de vie du panneau électrique affichant le score des concurrents ?
Déterminons maintenant
Comme nous avons une forme indéterminée nous transformons l'écriture :
Dans les calculs ci-après on n'oublie par que .
; et par composition : ; en multipliant par il vient : .
; ; par composition et en divisant par :
Finalement par addition :
Et donc
Dans le cas du panneau électrique l'espérance de durée de vie est h.
