Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2015 en Asie
Cacher les corrigés
Pour tout entier naturel , on définit la fonction pour tout réel de l'intervalle [0 ; 1] par :
On note la représentation graphique de la fonction dans un repère orthogonal.
Quelques-unes des courbes sont représentées ci-dessous.
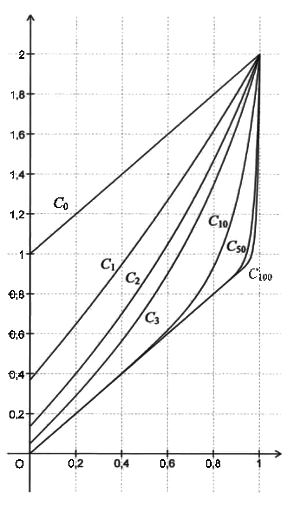
Partie A : généralités sur les fonctions
1. Démontrer que, pour tout entier naturel , la fonction est croissante et positive sur l'intervalle .
Pour tout entier naturel ; la fonction est dérivable sur et on a :
Comme ; et donc pour tout , , ce qui montre que est strictement croissante sur .
Positivité
Pour tout et tout ; et , donc la somme est strictement positive c'est à dire qu'on a .
2. Montrer que les courbes ont toutes un point commun A, et préciser ses coordonnées.
En observant le graphique on conjecture que le point A est le point de coordonnées .
Pour tout entier naturel , on calcule :
Donc pour tout entier naturel , la courbe passe par .
3. A l'aide des représentations graphiques, peut-on conjecturer le comportement des coefficients directeurs des tangentes en A aux courbes pour les grandes valeurs de ?
Démontrer cette conjecture.
On conjecture que le coefficient directeur augmente lorsque croît et que les tangentes tendent vers la « position verticale ».
Pour le montrer on considère :
Considérons la fonction définie sur par :
qui donne en fonction de , le coefficient directeur de la tangente à au point A.
Nous remarquons qu'il s'agit d'une fonction croissante dont la limite en est , ce qui montre notre conjecture.
Partie B : évolution de lorsque est fixé
Soit un réel fixé de l'intervalle . Pour tout entier naturel , on pose .
1. Dans cette question, on suppose que .
Etudier la limite éventuelle de la suite .
Pour ; nous avons :
Il s'agit d'une suite constante dont la limite est 2.
2. Dans cette question, on suppose que .
Etudier la limite éventuelle de la suite .
Pour :
Comme ; et donc .
; donc par composition .
Pour terminer, par somme : .
Partie C : aire sous les courbes
Pour tout entier naturel , on note l'aire, exprimée en unité d'aire, du domaine situé entre l'axe des abscisses, la courbe et les droites d'équations respectives et .
A partir des représentations graphiques, conjecturer la limite de la suite lorsque l'entier tend vers , puis démontrer cette conjecture.
On conjecture que l'aire du domaine tend vers l'aire du demi-carré de côté 1 ; donc que tend vers .
Il s'agit de calculer .
On commence par déterminer une primitive de : .
et donc par quotient .
Finalement par somme :
.
