Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2015 en métropole
Cacher les corrigés
1. Résoudre dans l'ensemble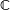 
des nombres complexes l'équation (E) d'inconnue 
:
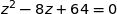
Le discriminant associé à l'équation est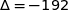 
.
Comme il est négatif, l'équation a deux solutions complexes conjuguées qui sont :
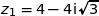et 
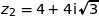
2. Le plan complexe est muni d'un repère orthonormé direct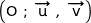 
.
On considère les points A, B et C d'affixes respectives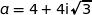 
,
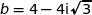et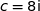 
.
a) Calculer le module et un argument du nombre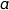 
.
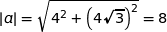
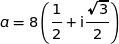
On cherche un argument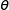 
tel que : 
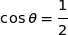et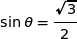 
, on prend 
.
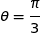b) Donner la forme exponentielle des nombres 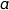et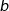 
.
En utilisant les résultats de la question précédente on a directement :
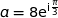
On remarque que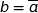 
, donc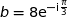 
c) Montrer que les points A, B et C sont sur un même cercle de centre O dont on déterminera le rayon.
.
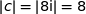Du coup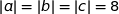 
: les points A, B et C sont sur le cercle de centre O et de rayon 8.
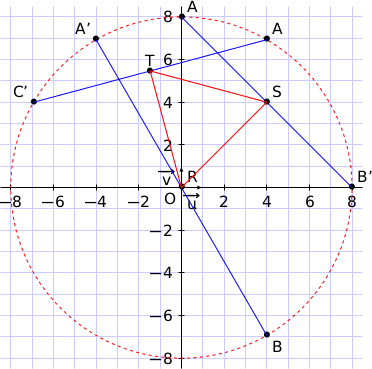
d) Placer les points A, B et C dans le repère .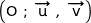
Pour la suite de l'exercice, on pourra s'aider de la figure de la question 2. d. complétée au fur et à mesure de l'avancement des questions.
3. On considère les points A
, B et C d'affixes respectives 
, 
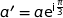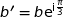et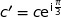 
.
a) Montrer que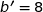 
.
.
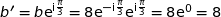b) Calculer le module et un argument du nombre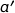 
.
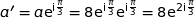
Module de 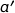: 8
Argument de :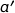 
.
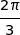Pour la suite on admet que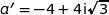 
et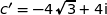 
.
4. On admet que si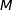 
et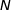 
sont deux points du plan d'affixes respectives 
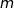et 
alors le milieu 
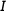du segment 
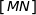a pour affixe 
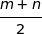et la longueur 
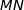est égale à 
.
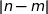a) On note 
, 
et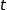 
les affixes des milieux respectifs R, S et T des segments [AB],: [BC] et [CA].
Calculer et . On admet que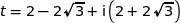 
.
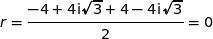
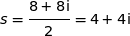
b) Quelle conjecture peut-on faire quant à la nature du triangle RST ?
Justifier ce résultat.
On conjecture que RST est équilatéral.
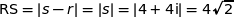
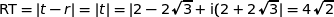
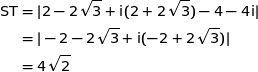
Donc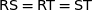 
: le triangle est équilatéral.
Figure complète :
