Sujet et corrigé de l'exercice 2 du bac S de maths de mai 2013 en Amérique du nord
Cacher les corrigés
On considère la suite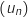
définie par 
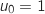et, pour tout entier naturel 
par :
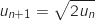
1. On considère l'algorithme suivant :
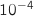près du résultat qu'affiche cet algorithme lorsque l'on choisit 
.
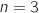En faisant tourner l'algorithme à la main avec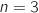 
, les variables prennent les valeurs succesives indiquées dans le tableau ci-dessous :
Donc l'algorithme affiche en sortie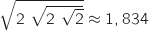 
b. Que permet de calculer cet algorithme ?
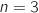, les variables prennent les valeurs succesives indiquées dans le tableau ci-dessous :
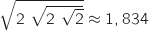
Cet algorithme calcule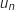 
pour la valeur de saisie par l'utilisateur.
c. Le tableau ci-dessous donne des valeurs approchées obtenues à l'aide de cet algorithme pour certaines valeurs de 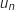pour la valeur de saisie par l'utilisateur.
.
?
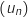On peut conjecturer que la suite 
est croissante et qu'elle converge vers 2.
est croissante et qu'elle converge vers 2.
2.a. Démontrer que, pour tout entier naturel
.
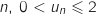On effectue une démonstration par récurrence de la propriété 
: « 
».
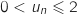Initialisation au rang 0
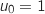et on a 
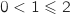, donc 
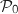est vraie.
Hérédité
On suppose que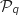 
est vraie, c'est à dire qu'on suppose avoir : 
.
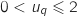On veut montrer qu'alors 
est également vraie.
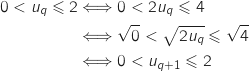Donc est vraie.
La propriété est initialisée au rang 0 ; elle est héréditaire ; donc elle est vraie pour tout entier naturel .
b. Déterminer le sens de variation de la suite : « ».
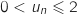Initialisation au rang 0
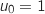et on a 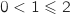, donc 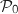est vraie.
Hérédité
On suppose que 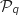est vraie, c'est à dire qu'on suppose avoir : .
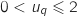On veut montrer qu'alors est également vraie.
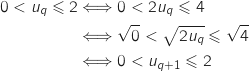Donc est vraie.
La propriété est initialisée au rang 0 ; elle est héréditaire ; donc elle est vraie pour tout entier naturel .
.
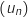Pour tout entier naturel , on peut écrire :
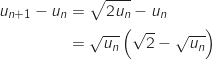De l'inégalité 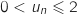on déduit 
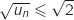(car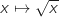 
est croissante sur 
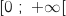) et donc 
.
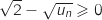Du coup,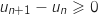 
ce qui montre que la suite est croissante.
c. Démontrer que la suite , on peut écrire :
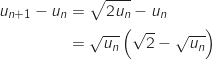De l'inégalité 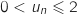on déduit 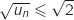(car 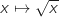est croissante sur 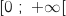) et donc .
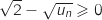Du coup, 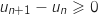ce qui montre que la suite est croissante.
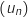est convergente. On ne demande pas la valeur de sa limite.
Dans les questions précédentes on a vu que la suite est croissante et qu'elle est majorée par 2 donc elle est convergente d'après le théorème de la convergence monotone.
3. On considère la suite est croissante et qu'elle est majorée par 2 donc elle est convergente d'après le théorème de la convergence monotone.
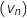définie, pour tout entier naturel , par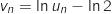 
.
a. Démontrer que la suite 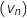est la suite géométrique de raison 
et de premier terme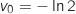 
.
Pour tout entier naturel :
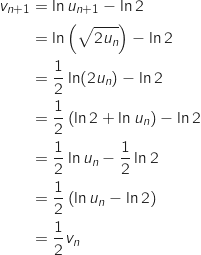Donc 
est une suite géométrique de raison .
Son premier terme est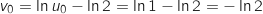 
.
b. Déterminer, pour tout entier naturel :
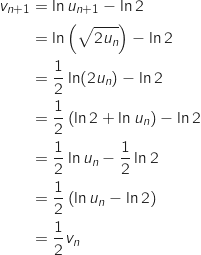Donc est une suite géométrique de raison .
Son premier terme est .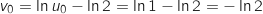
, l'expression de 
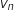en fonction de , puis de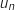 
en fonction de .
La suite étant géométrique de raison et de premier terme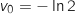 
, on a directement la formule explicite :
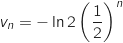et :
En remplaçant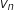 
par sa formule explicite il vient :
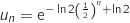
c. Déterminer la limite de la suite étant géométrique de raison et de premier terme 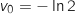, on a directement la formule explicite :
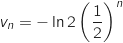et :
En remplaçant 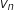par sa formule explicite il vient :
.
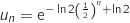
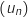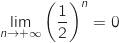car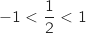 
;
par produit :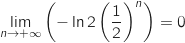 
;
en ajoutant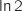 
: 
.
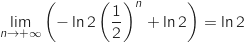Pour finir en composant avec l'exponentielle on obtient 
.
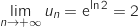telle que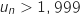 
.
On doit réaliser une boucle qui calcule les termes 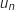de la suite tant que 
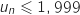ce qui donne :
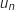de la suite tant que 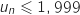ce qui donne :
