Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2013 aux Antilles
Cacher les corrigés
Dans tout ce qui suit,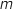 désigne un nombre réel quelconque.
désigne un nombre réel quelconque.
Partie A
Soit la fonction définie et dérivable sur l'ensemble des nombres réels
la fonction définie et dérivable sur l'ensemble des nombres réels 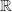 telle que :
telle que :
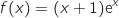
1. Calculer la limite de
 en
en  et en
et en  .
.
Limite en 
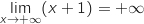 et
et
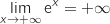 , donc
par produit
, donc
par produit 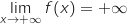 .
Limite en
.
Limite en  On a une forme indéterminée, mais pour tout
On a une forme indéterminée, mais pour tout  on peut écrire :
on peut écrire :
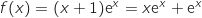 .
.
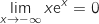 (limite connue).
(limite connue).
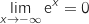 .
Donc par somme
.
Donc par somme 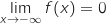 .
.
On note 
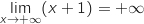 et
et
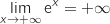 , donc
par produit
, donc
par produit 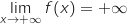 .
Limite en
.
Limite en  On a une forme indéterminée, mais pour tout
On a une forme indéterminée, mais pour tout  on peut écrire :
on peut écrire :
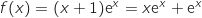 .
.
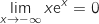 (limite connue).
(limite connue).
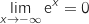 .
Donc par somme
.
Donc par somme 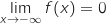 .
.
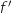 la fonction dérivée de la fonction
la fonction dérivée de la fonction  sur
sur  .
Démontrer que pour tout réel
.
Démontrer que pour tout réel 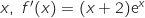 .
.
La fonction  est dérivable sur
est dérivable sur  et on a :
et on a :
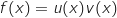 avec :
avec :
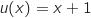 ;
; 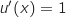
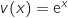 ;
; 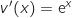
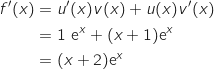
 est dérivable sur
est dérivable sur  et on a :
et on a :
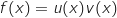 avec :
avec :
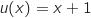 ;
; 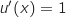
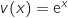 ;
; 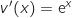
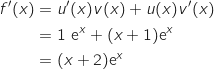
3. Dresser le tableau de variation de
 sur
sur  .
.
Pour tout  ,
, 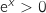 , donc le signe de
, donc le signe de  est le même
que celui de
est le même
que celui de 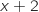 , ce qui donne le tableau de variations :
, ce qui donne le tableau de variations :
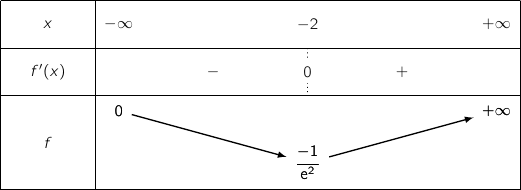
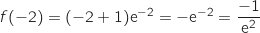
 ,
, 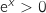 , donc le signe de
, donc le signe de  est le même
que celui de
est le même
que celui de 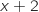 , ce qui donne le tableau de variations :
, ce qui donne le tableau de variations :

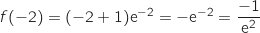
Partie B
On définit la fonction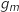 sur
sur  par
par
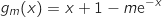
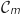 la courbe de la fonction
la courbe de la fonction 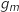 dans un repère
dans un repère 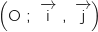 du plan.
1.a. Démontrer que
du plan.
1.a. Démontrer que 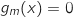 si et seulement si
si et seulement si 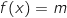 .
.
Pour tout  on a :
on a :
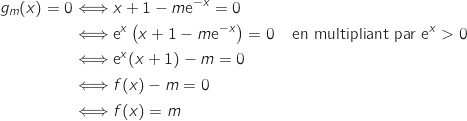
b. Déduire de la partie A, sans justification, le nombre de points d'intersection de la courbe  on a :
on a :
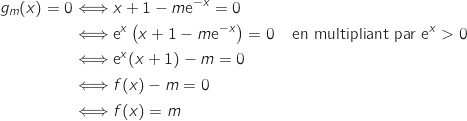
 avec l'axe des abscisses en fonction du réel
avec l'axe des abscisses en fonction du réel 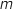 .
.
D'après la question précédente, le nombre de points d'intersection de la courbe
avec l'axe des abscisses coïncide avec le nombre de solutions de l'équation 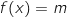 .
En exploitant le tableau de variations de la fonction
.
En exploitant le tableau de variations de la fonction  on obtient les résultats suivants :
on obtient les résultats suivants :
2. On a représenté ci-dessous les courbes 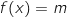 .
En exploitant le tableau de variations de la fonction
.
En exploitant le tableau de variations de la fonction  on obtient les résultats suivants :
on obtient les résultats suivants :
- pour
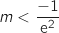 , aucune solution pour
, aucune solution pour 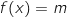 ,
aucun point d'intersection ;
,
aucun point d'intersection ;
- pour
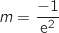 , une unique solution pour
, une unique solution pour 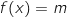 ,
un unique point d'intersection ;
,
un unique point d'intersection ;
- pour
 , deux solutions pour
, deux solutions pour 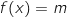 ,
deux points d'intersection ;
,
deux points d'intersection ;
- pour
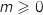 , une unique solution pour
, une unique solution pour 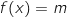 ,
un unique point d'intersection.
,
un unique point d'intersection.
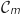 ,
, 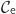 et
et 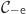 (obtenues en prenant respectivement pour
(obtenues en prenant respectivement pour 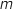 les valeurs
les valeurs 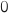 , e et
, e et 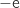 ).
).
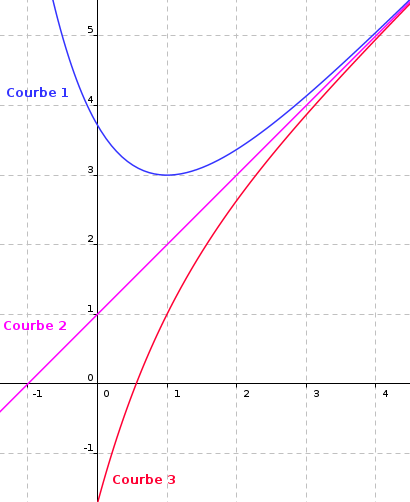
L'expression de 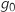 est :
est : 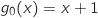 , c'est donc une fonction affine, sa courbe représentative est une droite, donc c'est
la courbe 2.
, c'est donc une fonction affine, sa courbe représentative est une droite, donc c'est
la courbe 2.
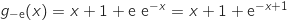 , dans ce cas
, dans ce cas 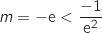 , donc
la courbe ne coupe pas l'axe des abscisses et du coup la seule possibilité est la courbe 1.
Par élimination la courbe de
, donc
la courbe ne coupe pas l'axe des abscisses et du coup la seule possibilité est la courbe 1.
Par élimination la courbe de 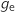 est la courbe 3.
est la courbe 3.
3. Etudier la position de la courbe 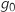 est :
est : 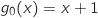 , c'est donc une fonction affine, sa courbe représentative est une droite, donc c'est
la courbe 2.
, c'est donc une fonction affine, sa courbe représentative est une droite, donc c'est
la courbe 2.
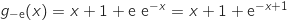 , dans ce cas
, dans ce cas 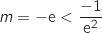 , donc
la courbe ne coupe pas l'axe des abscisses et du coup la seule possibilité est la courbe 1.
Par élimination la courbe de
, donc
la courbe ne coupe pas l'axe des abscisses et du coup la seule possibilité est la courbe 1.
Par élimination la courbe de 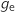 est la courbe 3.
est la courbe 3.
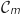 par rapport à la droite
par rapport à la droite  d'équation
d'équation 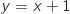 suivant les valeurs du réel
suivant les valeurs du réel 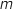 .
.
Il s'agit d'étudier le signe de 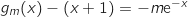 .
Pour tout
.
Pour tout  ,
, 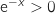 et le signe de l'expression considérée
est du signe contraire de
et le signe de l'expression considérée
est du signe contraire de 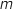 . Ainsi pour tout
. Ainsi pour tout  , on a :
, on a :
4.a. On appelle D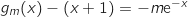 .
Pour tout
.
Pour tout  ,
, 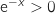 et le signe de l'expression considérée
est du signe contraire de
et le signe de l'expression considérée
est du signe contraire de 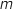 . Ainsi pour tout
. Ainsi pour tout  , on a :
, on a :
- pour
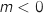 ,
, 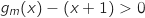 soit
soit 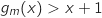 , donc
, donc 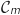 est
situé au dessus de la droite
est
situé au dessus de la droite  ;
;
- pour
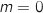 ,
, 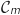 et
et  coïncident ;
coïncident ;
- pour
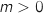 ,
, 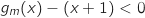 soit
soit 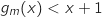 , donc
, donc
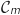 est situé en dessous de la droite
est situé en dessous de la droite  .
.
 la partie du plan comprise entre les courbes
la partie du plan comprise entre les courbes 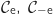 , l'axe (O
, l'axe (O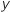 ) et la droite
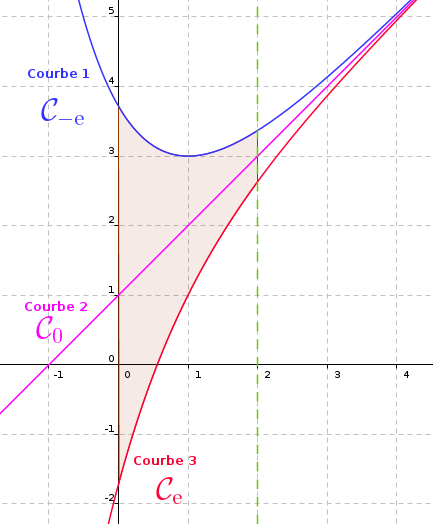
) et la droite 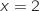 .
Hachurer D
.
Hachurer D sur le la figure.
sur le la figure.
 désigne un réel positif, D
désigne un réel positif, D la partie du plan comprise entre
la partie du plan comprise entre 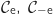 ,
l'axe (O
,
l'axe (O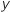 ) et la droite
) et la droite 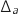 d'équation
d'équation 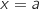 . On désigne par
. On désigne par 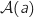 l'aire de cette partie du plan exprimée en unités d'aire.
Démontrer que pour tout réel a positif :
l'aire de cette partie du plan exprimée en unités d'aire.
Démontrer que pour tout réel a positif : 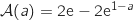 .
En déduire la limite de
.
En déduire la limite de 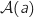 quand
quand  tend vers
tend vers 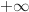 .
.
A partir de l'étude précédente, on peut dire que la courbe 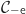 est située au dessus de
est située au dessus de  elle-même située au dessus de
elle-même située au dessus de 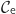 .
Donc
.
Donc 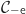 est située au dessus de
est située au dessus de 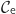 et du coup
pour tout réel
et du coup
pour tout réel 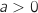 , on a :
, on a :
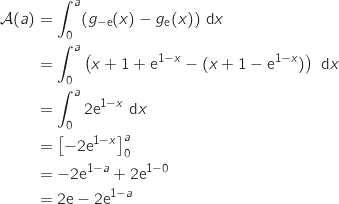
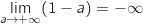 et
par composition
et
par composition 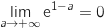 .
Du coup par somme :
.
Du coup par somme : 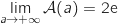 .
.
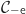 est située au dessus de
est située au dessus de  elle-même située au dessus de
elle-même située au dessus de 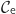 .
Donc
.
Donc 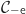 est située au dessus de
est située au dessus de 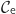 et du coup
pour tout réel
et du coup
pour tout réel 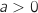 , on a :
, on a :
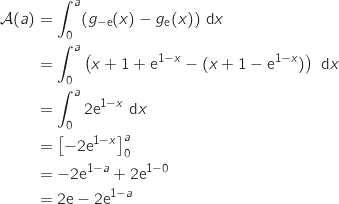
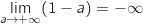 et
par composition
et
par composition 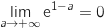 .
Du coup par somme :
.
Du coup par somme : 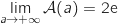 .
.
