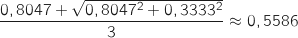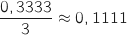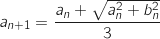Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2013 aux Antilles
Cacher les corrigés
On considère la suite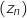 à termes complexes définie par :
à termes complexes définie par : 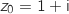 et, pour tout entier naturel
et, pour tout entier naturel  , par
, par
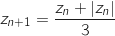
 , on pose :
, on pose : 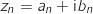 , où
, où 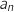 est la partie réelle de
est la partie réelle de 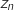 et
et 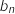 est la partie imaginaire de
est la partie imaginaire de 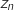 .
Le but de cet exercice est d'étudier la convergence des suites
.
Le but de cet exercice est d'étudier la convergence des suites 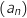 et
et 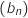 .
.
Partie A
1. Donner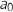 et
et 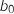 .
.
On sait que 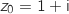 , donc
, donc 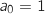 et
et 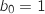 .
.
b. Calculer 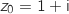 , donc
, donc 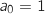 et
et 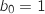 .
.
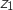 , puis en déduire que
, puis en déduire que 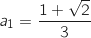 et
et 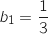 .
.
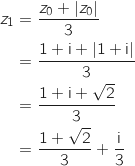 Du coup on a bien :
Du coup on a bien : 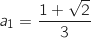 et
et 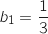 .
.

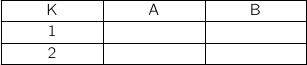
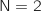 . Recopier et compléter le tableau ci-dessous contenant l'état des variables au cours de
l'exécution de l'algorithme (on arrondira les valeurs calculées à
. Recopier et compléter le tableau ci-dessous contenant l'état des variables au cours de
l'exécution de l'algorithme (on arrondira les valeurs calculées à 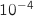 près).
près).

L'algorithme affiche le terme de rang N de la suite 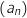 .
.
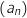 .
.
Partie B
1. Pour tout entier naturel , exprimer
, exprimer 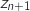 en fonction de
en fonction de 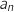 et
et 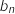 .
En déduire l'expression de
.
En déduire l'expression de 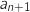 en fonction de
en fonction de 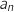 et
et 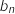 , et l'expression de
, et l'expression de 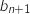 en fonction de
en fonction de 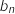 .
.
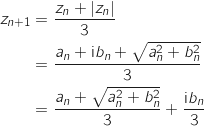 Donc on a pour tout entier naturel
Donc on a pour tout entier naturel  :
:
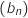 ? En déduire l'expression de
? En déduire l'expression de 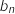 en fonction de
en fonction de  , et déterminer la limite de la suite
, et déterminer la limite de la suite 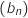 .
.
La relation 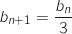 montre que
montre que 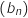 est une suite géométrique de raison
est une suite géométrique de raison
 .
Son premier terme est
.
Son premier terme est 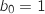 .
Sa formule explicite est
.
Sa formule explicite est 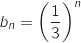 .
Comme
.
Comme 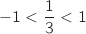 ,
, 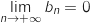 .
.
3.a. On rappelle que pour tous nombres complexes 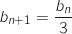 montre que
montre que 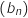 est une suite géométrique de raison
est une suite géométrique de raison
 .
Son premier terme est
.
Son premier terme est 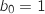 .
Sa formule explicite est
.
Sa formule explicite est 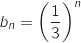 .
Comme
.
Comme 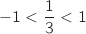 ,
, 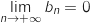 .
.
 et
et 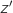 :
:
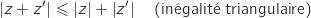
 ,
,
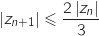
Pour tout entier naturel  :
:
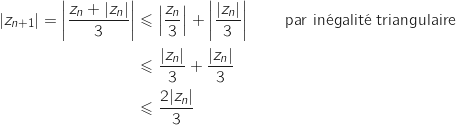
b. Pour tout entier naturel  :
:
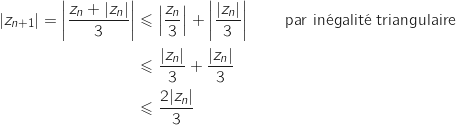
 , on pose
, on pose 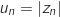 .
Montrer par récurrence que pour tout entier naturel
.
Montrer par récurrence que pour tout entier naturel  ,
,
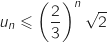
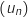 converge vers une limite que l'on déterminera.
converge vers une limite que l'on déterminera.
On considère la propriété  :
:
« 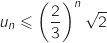 »
»
Initialisation au rang 0
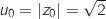 et
et 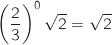 , donc
, donc 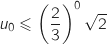 ce qui montre que
ce qui montre que 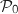 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 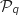 est vraie pour un entier
est vraie pour un entier  :
: 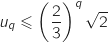 .
On remarque que la question a. précédente nous donne l'inégalité :
.
On remarque que la question a. précédente nous donne l'inégalité : 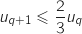 En multipliant par
En multipliant par  l'inégalité de l'hypothèse de récurrence on a :
l'inégalité de l'hypothèse de récurrence on a :
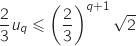 et du coup :
et du coup :
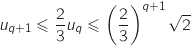 , ce
qui prouve que
, ce
qui prouve que  est vraie.
La propriété est donc héréditaire.
Ainsi
est vraie.
La propriété est donc héréditaire.
Ainsi  est vraie au rang 0, elle est héréditaire, donc elle
est vraie pour tout entier naturel
est vraie au rang 0, elle est héréditaire, donc elle
est vraie pour tout entier naturel  .
Comme
.
Comme 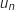 est un module on a
est un module on a 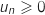 et donc pour tout entier naturel
et donc pour tout entier naturel  :
:
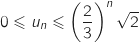 Comme
Comme 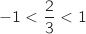 ,
, 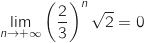 , donc
d'après le théorème des gendarmes,
, donc
d'après le théorème des gendarmes, 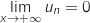 .
.
c. Montrer que, pour tout entier naturel  :
:
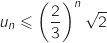 »
»
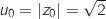 et
et 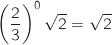 , donc
, donc 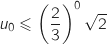 ce qui montre que
ce qui montre que 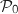 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 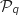 est vraie pour un entier
est vraie pour un entier  :
: 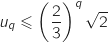 .
On remarque que la question a. précédente nous donne l'inégalité :
.
On remarque que la question a. précédente nous donne l'inégalité : 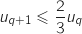 En multipliant par
En multipliant par  l'inégalité de l'hypothèse de récurrence on a :
l'inégalité de l'hypothèse de récurrence on a :
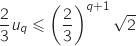 et du coup :
et du coup :
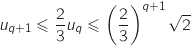 , ce
qui prouve que
, ce
qui prouve que  est vraie.
La propriété est donc héréditaire.
Ainsi
est vraie.
La propriété est donc héréditaire.
Ainsi  est vraie au rang 0, elle est héréditaire, donc elle
est vraie pour tout entier naturel
est vraie au rang 0, elle est héréditaire, donc elle
est vraie pour tout entier naturel  .
Comme
.
Comme 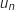 est un module on a
est un module on a 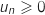 et donc pour tout entier naturel
et donc pour tout entier naturel  :
:
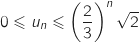 Comme
Comme 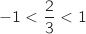 ,
, 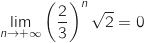 , donc
d'après le théorème des gendarmes,
, donc
d'après le théorème des gendarmes, 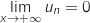 .
.
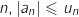 .
En déduire que la suite
.
En déduire que la suite 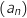 converge vers une limite que l'on déterminera.
converge vers une limite que l'on déterminera.
Pour tout entier naturel  :
:
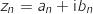 donc
donc 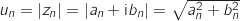 On a :
On a : 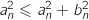 , car
, car 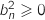 , puis :
, puis :
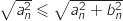 , (fonction racine croissante sur
, (fonction racine croissante sur  )
Cette inégalité correspond exactement à
)
Cette inégalité correspond exactement à 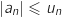 .
Ainsi :
.
Ainsi : 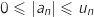 , avec
, avec 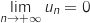 , donc d'après le
théorème des gendarmes,
, donc d'après le
théorème des gendarmes, 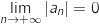 ce
qui entraîne que
ce
qui entraîne que 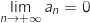 .
.
 :
:
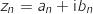 donc
donc 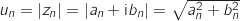 On a :
On a : 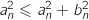 , car
, car 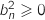 , puis :
, puis :
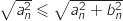 , (fonction racine croissante sur
, (fonction racine croissante sur  )
Cette inégalité correspond exactement à
)
Cette inégalité correspond exactement à 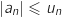 .
Ainsi :
.
Ainsi : 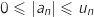 , avec
, avec 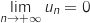 , donc d'après le
théorème des gendarmes,
, donc d'après le
théorème des gendarmes, 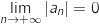 ce
qui entraîne que
ce
qui entraîne que 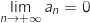 .
.