Corrigé de l'exercice 1 du bac S de maths de juin 2012 en Asie
Cacher les corrigés
Pour chaque question, une affirmation est proposée. Indiquer si cette affirmation est vraie ou fausse, en justifiant la réponse. Une réponse correcte et justifiée rapporte 1 point. 1. Dans l'espace rapporté à un repère orthonormal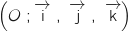 ,
on considère la droite
,
on considère la droite  dont on donne une représentation paramétrique, et le plan
dont on donne une représentation paramétrique, et le plan  dont on donne une équation cartésienne :
dont on donne une équation cartésienne :
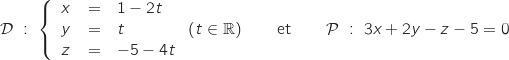
 est strictement parallèle au plan
est strictement parallèle au plan  .
.
Par lecture directe sur la représentation paramétrique de  , un vecteur directeur de cette droite est
, un vecteur directeur de cette droite est 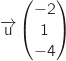 .
Par lecture directe sur l'équation cartésienne de
.
Par lecture directe sur l'équation cartésienne de  , un vecteur normal de ce plan est
, un vecteur normal de ce plan est 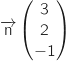 .
On a de plus :
.
On a de plus : 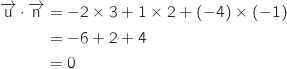 Donc
Donc 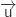 et
et  sont orthogonaux, ce qui prouve que la droite
sont orthogonaux, ce qui prouve que la droite  est parallèle à
est parallèle à  .
En remplaçant
.
En remplaçant 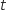 par 0 dans la représentation paramétrique de
par 0 dans la représentation paramétrique de  , on obtient le point
, on obtient le point 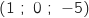 , et ce point n'appartient pas à
, et ce point n'appartient pas à  car :
car :
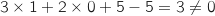 Du coup
Du coup  n'est pas inclue dans
n'est pas inclue dans  et
et  est strictement parallèle à
est strictement parallèle à  .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
2. Dans l'espace rapporté à un repère orthonormal  , un vecteur directeur de cette droite est
, un vecteur directeur de cette droite est 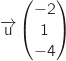 .
Par lecture directe sur l'équation cartésienne de
.
Par lecture directe sur l'équation cartésienne de  , un vecteur normal de ce plan est
, un vecteur normal de ce plan est 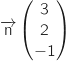 .
On a de plus :
.
On a de plus : 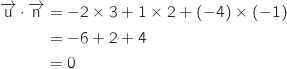 Donc
Donc 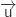 et
et  sont orthogonaux, ce qui prouve que la droite
sont orthogonaux, ce qui prouve que la droite  est parallèle à
est parallèle à  .
En remplaçant
.
En remplaçant 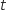 par 0 dans la représentation paramétrique de
par 0 dans la représentation paramétrique de  , on obtient le point
, on obtient le point 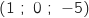 , et ce point n'appartient pas à
, et ce point n'appartient pas à  car :
car :
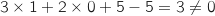 Du coup
Du coup  n'est pas inclue dans
n'est pas inclue dans  et
et  est strictement parallèle à
est strictement parallèle à  .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
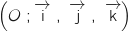 ,
on considère le point A
,
on considère le point A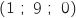 et le plan
et le plan  d'équation cartésienne :
d'équation cartésienne : 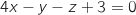 .
On rappelle que la distance
.
On rappelle que la distance 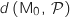 du point
du point 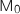 au plan
au plan  d'équation
d'équation 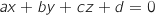 est donnée par :
est donnée par :
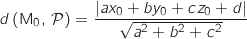
 est égale à
est égale à 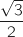 .
.
En utilisant la formule rappelée on a directement :
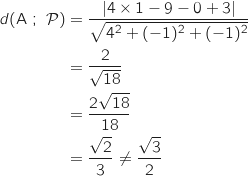 Donc l'affirmation est FAUSSE.
Donc l'affirmation est FAUSSE.
3. Soit la fonction 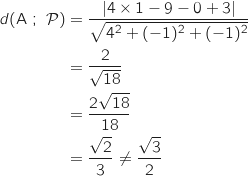 Donc l'affirmation est FAUSSE.
Donc l'affirmation est FAUSSE.
 définie pour tout réel
définie pour tout réel  par :
par : 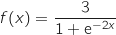 .
On note
.
On note  la courbe représentative de la fonction
la courbe représentative de la fonction  dans un repère du plan.
Affirmation 3
La courbe
dans un repère du plan.
Affirmation 3
La courbe  admet deux asymptotes parallèles à l'axe des abscisses.
admet deux asymptotes parallèles à l'axe des abscisses.
Pour savoir si la courbe  admet deux asymptotes « horizontales » il faut déterminer les limites à l'infini.
Limite en
admet deux asymptotes « horizontales » il faut déterminer les limites à l'infini.
Limite en 
 , l'axe des abscisses est asymptote à
, l'axe des abscisses est asymptote à  .
Limite en
.
Limite en 
 ,
,  admet pour asymptote la droite d'équation
admet pour asymptote la droite d'équation 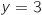 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
4. Pour tout réel  admet deux asymptotes « horizontales » il faut déterminer les limites à l'infini.
Limite en
admet deux asymptotes « horizontales » il faut déterminer les limites à l'infini.
Limite en 
-
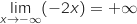 et par composition
et par composition 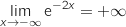
- Par somme :
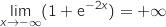
- Enfin, par quotient :
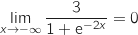 .
.
 , l'axe des abscisses est asymptote à
, l'axe des abscisses est asymptote à  .
Limite en
.
Limite en 
-
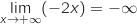 et par composition
et par composition 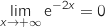
- Par somme :
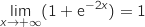
- Enfin, par quotient :
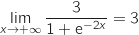 .
.
 ,
,  admet pour asymptote la droite d'équation
admet pour asymptote la droite d'équation 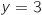 .
L'affirmation est VRAIE.
.
L'affirmation est VRAIE.
 , on pose
, on pose 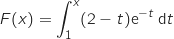 .
Affirmation 4
.
Affirmation 4
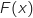 est négatif ou nul quelle que soit la valeur du réel
est négatif ou nul quelle que soit la valeur du réel  supérieur à 1.
supérieur à 1.
Si on prend, par exemple, 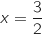 , on a
, on a 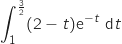 avec la fonction
avec la fonction
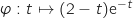 qui est strictement positive pour tout
qui est strictement positive pour tout 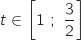 , donc l'intégrale est aussi strictement positive.
L'affirmation est FAUSSE.
, donc l'intégrale est aussi strictement positive.
L'affirmation est FAUSSE.
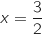 , on a
, on a 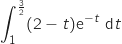 avec la fonction
avec la fonction
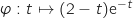 qui est strictement positive pour tout
qui est strictement positive pour tout 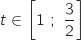 , donc l'intégrale est aussi strictement positive.
L'affirmation est FAUSSE.
, donc l'intégrale est aussi strictement positive.
L'affirmation est FAUSSE.
Il y avait une dernière question dans ce sujet, mais elle nécessite l'utilisation d'une intégration par parties qui ne fait plus partie du programme à compter de la rentrée 2012/2013.
