Corrigé de l'exercice 3 du bac S de maths de juin 2012 en Asie
Cacher les corrigés
Soit un entier naturel supérieur ou égal à 2.
Une urne contient
un entier naturel supérieur ou égal à 2.
Une urne contient  boules noires et 3 boules blanches.
Ces
boules noires et 3 boules blanches.
Ces 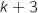 boules sont indiscernables au toucher.
Une partie consiste à prélever au hasard successivement et avec remise deux boules dans cette urne.
On établit la règle de jeu suivante :
boules sont indiscernables au toucher.
Une partie consiste à prélever au hasard successivement et avec remise deux boules dans cette urne.
On établit la règle de jeu suivante :
- un joueur perd 9 euros si les deux boules tirées sont de couleur blanche ;
- un joueur perd 1 euro si les deux boules tirées sont de couleur noire ;
- un joueur gagne 5 euros si les deux boules tirées sont de couleurs différentes ; on dit dans ce cas là qu'il gagne la partie.
Partie A
Dans la partie A, on pose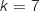 .
Ainsi l'urne contient 3 boules blanches et 7 boules noires indiscernables au toucher.
1. Un joueur joue une partie. On note
.
Ainsi l'urne contient 3 boules blanches et 7 boules noires indiscernables au toucher.
1. Un joueur joue une partie. On note 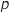 la probabilité que le joueur gagne la partie, c'est-à-dire la probabilité qu'il ait tiré deux boules de couleurs différentes.
Démontrer que
la probabilité que le joueur gagne la partie, c'est-à-dire la probabilité qu'il ait tiré deux boules de couleurs différentes.
Démontrer que 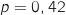 .
.
On peut représenter la situation par un arbre de probabilités en tenant compte du fait que les tirages se font avec remise.
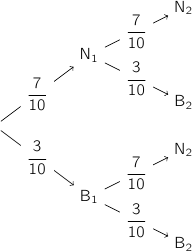
N désigne l'événement : « la première boule tirée est noire » ;
N
désigne l'événement : « la première boule tirée est noire » ;
N désigne l'évévénement : « la deuxième boule tirée est noire » ;
B
désigne l'évévénement : « la deuxième boule tirée est noire » ;
B désigne l'événement : « la première boule tirée est blanche » ;
B
désigne l'événement : « la première boule tirée est blanche » ;
B désigne l'évévénement : « la deuxième boule tirée est blanche ».
Il s'agit de calculer la probabilité de l'événement :
désigne l'évévénement : « la deuxième boule tirée est blanche ».
Il s'agit de calculer la probabilité de l'événement : 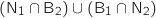 .
Comme
.
Comme 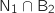 et
et 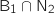 sont incompatibles il vient :
sont incompatibles il vient :
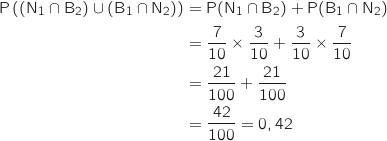

 désigne l'événement : « la première boule tirée est noire » ;
N
désigne l'événement : « la première boule tirée est noire » ;
N désigne l'évévénement : « la deuxième boule tirée est noire » ;
B
désigne l'évévénement : « la deuxième boule tirée est noire » ;
B désigne l'événement : « la première boule tirée est blanche » ;
B
désigne l'événement : « la première boule tirée est blanche » ;
B désigne l'évévénement : « la deuxième boule tirée est blanche ».
Il s'agit de calculer la probabilité de l'événement :
désigne l'évévénement : « la deuxième boule tirée est blanche ».
Il s'agit de calculer la probabilité de l'événement : 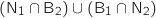 .
Comme
.
Comme 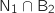 et
et 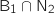 sont incompatibles il vient :
sont incompatibles il vient :
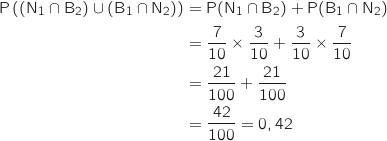
2. Soit
 un entier tel que
un entier tel que 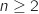 . Un joueur joue
. Un joueur joue  parties identiques et indépendantes.
On note
parties identiques et indépendantes.
On note  la variable aléatoire qui comptabilise le nombre de parties gagnées par le joueur, et
la variable aléatoire qui comptabilise le nombre de parties gagnées par le joueur, et 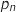 la probabilité que le joueur gagne au moins une fois au cours des
la probabilité que le joueur gagne au moins une fois au cours des  parties.
a. Expliquer pourquoi la variable
parties.
a. Expliquer pourquoi la variable  suit une loi binomiale de paramètres
suit une loi binomiale de paramètres  et
et 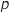 .
.
On répète de façon indépendante  fois une expérience de Bernoulli dont la probabilité du succès est
fois une expérience de Bernoulli dont la probabilité du succès est 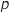 .
Donc la variabale aléatoire
.
Donc la variabale aléatoire  qui compte le nombre de succès suit une loi binomiale
qui compte le nombre de succès suit une loi binomiale 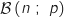 .
.
b. Exprimer  fois une expérience de Bernoulli dont la probabilité du succès est
fois une expérience de Bernoulli dont la probabilité du succès est 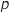 .
Donc la variabale aléatoire
.
Donc la variabale aléatoire  qui compte le nombre de succès suit une loi binomiale
qui compte le nombre de succès suit une loi binomiale 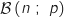 .
.
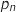 en fonction de
en fonction de  , puis calculer
, puis calculer 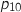 , en arrondissant au millième.
, en arrondissant au millième.
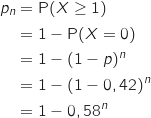 Donc
Donc 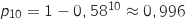 .
.
On cherche  tel que :
tel que :
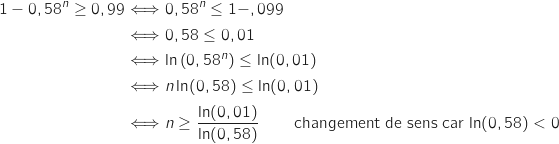 avec
avec 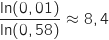 Donc il faut au moins jouer 9 parties.
Donc il faut au moins jouer 9 parties.
 tel que :
tel que :
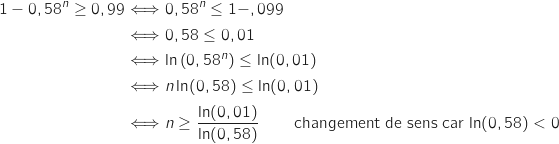 avec
avec 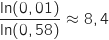 Donc il faut au moins jouer 9 parties.
Donc il faut au moins jouer 9 parties.
Partie B
Dans la partie B, le nombre est un entier naturel supérieur ou égal à 2.
Un joueur joue une partie.
On note
est un entier naturel supérieur ou égal à 2.
Un joueur joue une partie.
On note 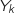 la variable aléatoire égale au gain algébrique du joueur.
1.a. Justifier l'égalité :
la variable aléatoire égale au gain algébrique du joueur.
1.a. Justifier l'égalité : 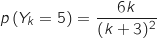 .
b. Ecrire la loi de probabilité de la variable aléatoire
.
b. Ecrire la loi de probabilité de la variable aléatoire 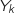 .
.
On fait un arbre comme dans la question A.1.
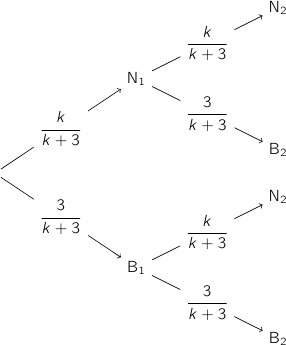
Les gains algébriques possibles sont :
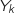 :
:
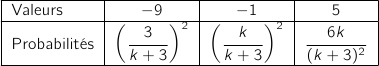
2. On note E
-
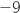 : quand l'événement
: quand l'événement 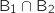 est réalisé.
est réalisé.
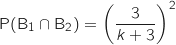 (principe multiplicatif sur l'arbre)
(principe multiplicatif sur l'arbre)
-
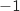 : quand l'événement
: quand l'événement 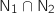 est réalisé.
est réalisé.
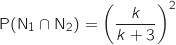 .
.
-
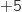 : quand l'événement
: quand l'événement 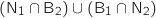 est réalisé.
est réalisé.
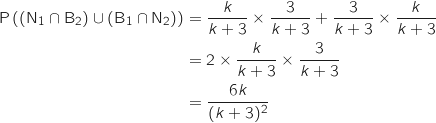
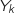 :
:
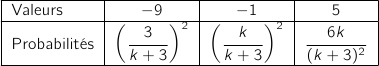
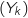 l'espérance mathématique de la variable aléatoire
l'espérance mathématique de la variable aléatoire 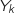 .
On dit que le jeu est favorable au joueur lorsque l'espérance E
.
On dit que le jeu est favorable au joueur lorsque l'espérance E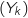 est strictement positive.
Déterminer les valeurs de
est strictement positive.
Déterminer les valeurs de  pour lesquelles ce jeu est favorable au joueur.
pour lesquelles ce jeu est favorable au joueur.
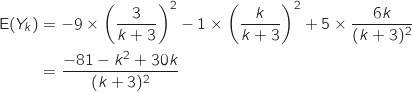 Pour
Pour 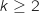 ; E
; E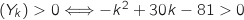 .
On étudie donc le signe du trinôme du second degré en question.
Son discriminant est
.
On étudie donc le signe du trinôme du second degré en question.
Son discriminant est 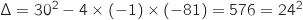 .
Il admet donc deux racines qui sont :
.
Il admet donc deux racines qui sont : 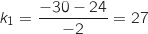 et
et 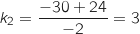 On en déduit son signe pour
On en déduit son signe pour 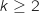 :
:

 entier de 4 à 26 inclus.
entier de 4 à 26 inclus.
