Sujet et corrigé de l'exercice de spécialité du bac S de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
Une espèce d'oiseaux ne vit que sur deux îles A et B d'un archipel. Au début de l'année 2013, 20 millions d'oiseaux de cette espèce sont présents sur l'île A et 10 millions sur l'île B. Des observations sur plusieurs années ont permis aux ornithologues d'estimer que, compte tenu des naissances, décès, et migrations entre les deux îles, on retrouve au début de chaque année les proportions suivantes :- sur l'île A : 80 % du nombre d'oiseaux présents sur l'île A au début de l'année précédente et 30 % du nombre d'oiseaux présents sur l'île B au début de l'année précédente ;
- sur l'île B : 20 % du nombre d'oiseaux présents sur l'île A au début de l'année précédente et 70 % du nombre d'oiseaux présents sur l'île B au début de l'année précédente.
Pour tout entier naturel
 , on note
, on note 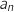 (respectivement
(respectivement 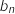 ) le nombre d'oiseaux (en millions) présents sur l'île A (respectivement B) au début de l'année
) le nombre d'oiseaux (en millions) présents sur l'île A (respectivement B) au début de l'année 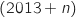 .
.
Partie A - Algorithmique et conjectures
On donne ci-dessous un algorithme qui doit afficher le nombre d'oiseaux vivant le nombre d'oiseaux vivant sur chacune des deux îles, pour chaque année comprise entre 2013 et une année choisie par l'utilisateur.
Le calcul des termes successifs de la suite est correctement assuré. On pourra
noter l'emploi indispensable de la variable auxiliaire  pour conserver
pour conserver  intact
pour le calcul de
intact
pour le calcul de  .
En revanche la variable
.
En revanche la variable 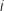 n'est pas incrémentée à chaque étape, donc il faudra rajouter
cette instruction (en l'état l'algorithme proposé génère une boucle infinie si l'utilisateur
entre une valeur
n'est pas incrémentée à chaque étape, donc il faudra rajouter
cette instruction (en l'état l'algorithme proposé génère une boucle infinie si l'utilisateur
entre une valeur 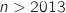 ).
Enfin, il manque les instructions d'affichage dans la boucle.
).
Enfin, il manque les instructions d'affichage dans la boucle.

 pour conserver
pour conserver  intact
pour le calcul de
intact
pour le calcul de  .
En revanche la variable
.
En revanche la variable 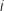 n'est pas incrémentée à chaque étape, donc il faudra rajouter
cette instruction (en l'état l'algorithme proposé génère une boucle infinie si l'utilisateur
entre une valeur
n'est pas incrémentée à chaque étape, donc il faudra rajouter
cette instruction (en l'état l'algorithme proposé génère une boucle infinie si l'utilisateur
entre une valeur 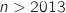 ).
Enfin, il manque les instructions d'affichage dans la boucle.
).
Enfin, il manque les instructions d'affichage dans la boucle.

2. On donne ci-dessous une copie d'écran des résultats obtenus après avoir corrigé l'algorithme précédent dans un logiciel d'algorithmique, l'utilisateur avant choisi l'année 2020.

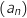 et
et 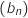 .
.
La suite 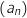 semble décroissante et converger vers 18.
La suite
semble décroissante et converger vers 18.
La suite 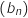 semble croissante et converger vers 12.
semble croissante et converger vers 12.
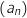 semble décroissante et converger vers 18.
La suite
semble décroissante et converger vers 18.
La suite 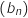 semble croissante et converger vers 12.
semble croissante et converger vers 12.
Partie B - Etude mathématique
On note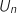 la matrice colonne
la matrice colonne 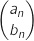 .
1. Montrer que, pour tout entier naturel
.
1. Montrer que, pour tout entier naturel  ,
, 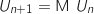 , où M est une matrice carrée d'ordre 2 que l'on déterminera.
On admet alors que
, où M est une matrice carrée d'ordre 2 que l'on déterminera.
On admet alors que 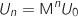 pour tout entier naturel
pour tout entier naturel  .
.
D'après l'énoncé on a les relations de récurrence :
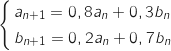 Du coup, on cherche à compléter la matrice pour avoir l'égalité :
Du coup, on cherche à compléter la matrice pour avoir l'égalité :
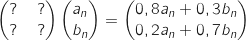 Pour réaliser cela il faut prendre
Pour réaliser cela il faut prendre 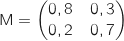
2. A l'aide d'un raisonnement par récurrence, justifier que, pour tout entier naturel 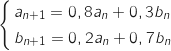 Du coup, on cherche à compléter la matrice pour avoir l'égalité :
Du coup, on cherche à compléter la matrice pour avoir l'égalité :
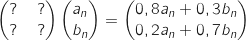 Pour réaliser cela il faut prendre
Pour réaliser cela il faut prendre 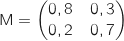
 :
:
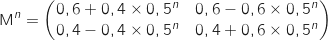
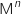 .
.
Initialisation au rang 1
En remplaçant  par 1 dans l'expression donnée il vient :
par 1 dans l'expression donnée il vient :
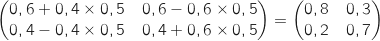 Ce qui donne M, donc la propriété est vraie pour
Ce qui donne M, donc la propriété est vraie pour 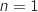 .
Hérédité
On suppose qu'à un rang
.
Hérédité
On suppose qu'à un rang 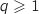 on a :
on a :
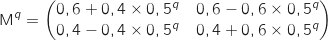 A partir de cela on calcule
A partir de cela on calcule 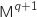 :
:
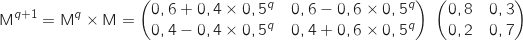 Comme indiqué dans l'énoncé on ne calcule que le premier coefficient :
Comme indiqué dans l'énoncé on ne calcule que le premier coefficient :
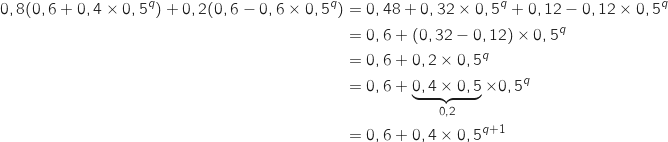 Donc l'hérédité est assurée pour ce premier coefficient, on admet qu'il en est de même
pour les autres.
Ainsi notre propriété est vérifiée au rang 1, elle est héréditaire, donc elle est
vraie pour tout entier
Donc l'hérédité est assurée pour ce premier coefficient, on admet qu'il en est de même
pour les autres.
Ainsi notre propriété est vérifiée au rang 1, elle est héréditaire, donc elle est
vraie pour tout entier  .
.
3. Exprimer  par 1 dans l'expression donnée il vient :
par 1 dans l'expression donnée il vient :
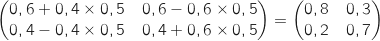 Ce qui donne M, donc la propriété est vraie pour
Ce qui donne M, donc la propriété est vraie pour 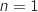 .
Hérédité
On suppose qu'à un rang
.
Hérédité
On suppose qu'à un rang 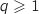 on a :
on a :
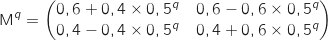 A partir de cela on calcule
A partir de cela on calcule 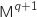 :
:
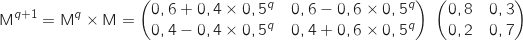 Comme indiqué dans l'énoncé on ne calcule que le premier coefficient :
Comme indiqué dans l'énoncé on ne calcule que le premier coefficient :
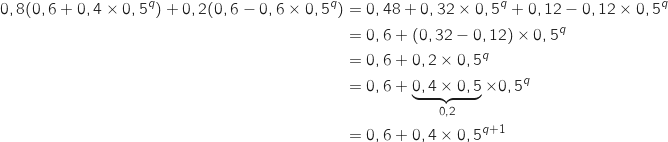 Donc l'hérédité est assurée pour ce premier coefficient, on admet qu'il en est de même
pour les autres.
Ainsi notre propriété est vérifiée au rang 1, elle est héréditaire, donc elle est
vraie pour tout entier
Donc l'hérédité est assurée pour ce premier coefficient, on admet qu'il en est de même
pour les autres.
Ainsi notre propriété est vérifiée au rang 1, elle est héréditaire, donc elle est
vraie pour tout entier  .
.
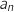 en fonction de
en fonction de  , pour tout entier naturel
, pour tout entier naturel  .
.
Comme 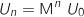 , pour avoir
, pour avoir 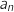 , on calcule le premier coefficient de :
, on calcule le premier coefficient de :
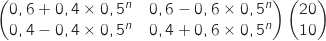 ce qui donne :
ce qui donne :
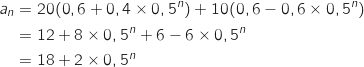
4. Avec ce modèle, peut-on dire qu'au bout d'un grand nombre d'années, le nombre d'oiseaux sur l'île A va se stabiliser ? Si oui, préciser vers quelle valeur.
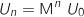 , pour avoir
, pour avoir 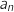 , on calcule le premier coefficient de :
, on calcule le premier coefficient de :
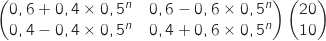 ce qui donne :
ce qui donne :
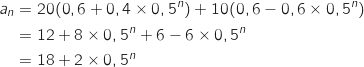
A l'aide de la formule explicite de 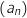 trouvée à la question précédente on calcule sa limite :
trouvée à la question précédente on calcule sa limite :
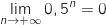 car
car 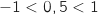 et du coup
et du coup
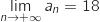 .
On peut dire qu'au fil du temps la population d'oiseaux sur l'île A
va avoir tendance à se stabiliser vers 18 millions d'animaux.
.
On peut dire qu'au fil du temps la population d'oiseaux sur l'île A
va avoir tendance à se stabiliser vers 18 millions d'animaux.
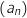 trouvée à la question précédente on calcule sa limite :
trouvée à la question précédente on calcule sa limite :
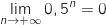 car
car 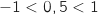 et du coup
et du coup
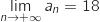 .
On peut dire qu'au fil du temps la population d'oiseaux sur l'île A
va avoir tendance à se stabiliser vers 18 millions d'animaux.
.
On peut dire qu'au fil du temps la population d'oiseaux sur l'île A
va avoir tendance à se stabiliser vers 18 millions d'animaux.
