Corrigé de l'exercice 1 de maths du bac S de juin 2011 en métropole
Cacher les corrigés
Les deux parties A et B peuvent être traitées indépendamment. Les résultats seront donnés sous forme décimale en arrondissant à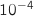
.
Dans un pays, il y a 2 % de la population contaminée par un virus.
PARTIE A
On dispose d'un test de dépistage de ce virus qui a les propriétés suivantes :- La probabilité qu'une personne contaminée ait un test positif est de
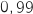(sensibilité du test).
- La probabilité qu'une personne non contaminée ait un test négatif est de
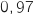(spécificité du test).
On note V l'évènement « la personne est contaminée par le virus » et T l'évènement « le test est positif ».
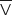et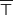 
désignent respectivement les évènements contraires de V et T.
1.a. Préciser les valeurs des probabilités
.
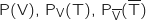En lisant l'énoncé on a directement :
.
.
.
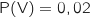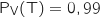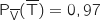Traduire la situation à l'aide d'un arbre de probabilités.
.
.
.
.
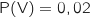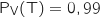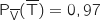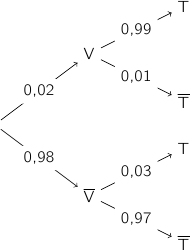
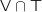D'après la formule des probabilités composées (principe mutliplicatif sur l'arbre) :
.
.
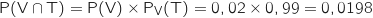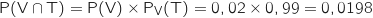2. Démontrer que la probabilité que le test soit positif est 0,0492.
D'après la formule des probabilités totales appliquée avec le système complet d'événements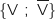 
on a :
.
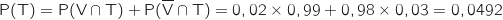3.a Justifier par un calcul la phrase :
« Si le test est positif, il n'y a qu'environ 40 % de "chances" que la personne soit contaminée ».
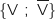on a :
.
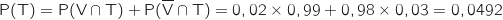En utilisant la définition des probabilités conditionnelles on a :
.
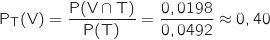Ce qui correspond aux environ 40 % de la phrase.
b. Déterminer la probabilité qu'une personne ne soit pas contaminée par le virus sachant que son test est négatif.
.
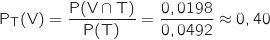Ce qui correspond aux environ 40 % de la phrase.
De nouveau on utilise la définition des probabilités conditionnelles :
.
.
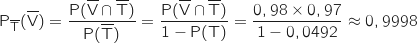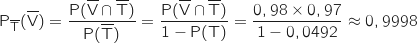PARTIE B
On choisit successivement 10 personnes de la population au hasard, on considère que les tirages sont indépendants.On appelle
la variable aléatoire qui donne le nombre de personnes contaminées par le virus parmi ces 10 personnes.
1. Justifier que suit une loi binomiale dont on donnera les paramètres.
On considère l'expérience qui consiste à observer si une personne tirée au sort est contaminée ou non, la probabilité qu'elle le soit est 0,02.
On répète cette expérience 10 fois de suite et de manière indépendante, donc la variable aléatoire qui compte le nombre de personnes contaminées suit une loi binomiale de paramètres 10 et 0,02.
2. Calculer la probabilité qu'il y ait au moins deux personnes contaminées parmi les 10.
qui compte le nombre de personnes contaminées suit une loi binomiale de paramètres 10 et 0,02.
La probabilité qu'il n'y ait aucune personne contaminée est :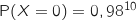 
.
La probabilité qu'il y ait exactement une personne contaminée est :
.
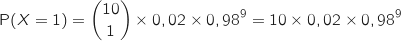En utilisant l'événement contraire, la probabilité cherchée dans cette question est :
.
.
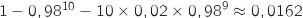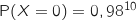La probabilité qu'il y ait exactement une personne contaminée est :
.
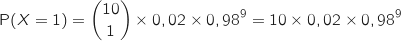En utilisant l'événement contraire, la probabilité cherchée dans cette question est :
.
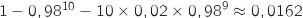