Corrigé de l'exercice 3 de maths du bac S de juin 2011 en métropole
Cacher les corrigés
Pour tout entier naturel supérieur ou égal à 1, on désigne par
supérieur ou égal à 1, on désigne par 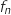 la fonction définie sur
la fonction définie sur  par :
par :
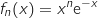
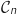 sa courbe représentative dans un repère orthogonal
sa courbe représentative dans un repère orthogonal 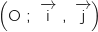 du plan.
du plan.
PARTIE A
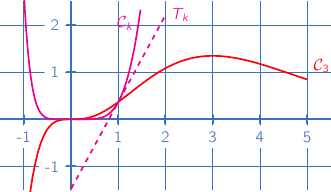
Sur le graphique ci-dessous, on a représenté une courbe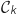 où
où  est un entier naturel non nul, sa tangente
est un entier naturel non nul, sa tangente 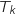 au point d'abscisse 1 et la courbe
au point d'abscisse 1 et la courbe 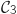 ·
La droite
·
La droite 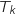 coupe l'axe des abscisses au point A de coordonnées
coupe l'axe des abscisses au point A de coordonnées 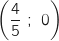 .
.
1.a. Déterminer les limites de la fonction
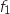 en
en 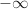 et en
et en 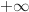 .
.
Limite en 
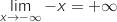 et par composition
et par composition 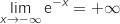 Donc par produit
Donc par produit 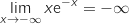 .
Limite en
.
Limite en  On a une forme indéterminée, cependant on peut écrire pour tout
On a une forme indéterminée, cependant on peut écrire pour tout  :
: 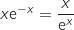 .
.
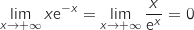 (par la propriété des croissances comparées).
(par la propriété des croissances comparées).
b. Etudier les variations de la fonction 
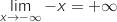 et par composition
et par composition 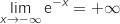 Donc par produit
Donc par produit 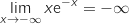 .
Limite en
.
Limite en  On a une forme indéterminée, cependant on peut écrire pour tout
On a une forme indéterminée, cependant on peut écrire pour tout  :
: 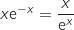 .
.
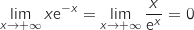 (par la propriété des croissances comparées).
(par la propriété des croissances comparées).
 et dresser le tableau de variations de
et dresser le tableau de variations de 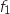 .
.
On obtient le tableau de variations suivant :
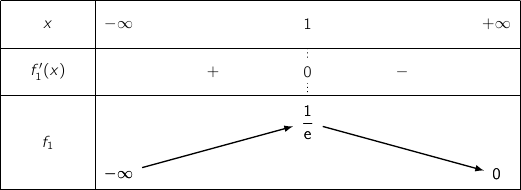

c. A l'aide du graphique, justifier que
 est un entier supérieur ou égal à 2.
est un entier supérieur ou égal à 2.
La courbe 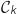 ne peut pas être la courbe représentative de
ne peut pas être la courbe représentative de 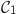 , car ce que « l'on voit » n'est cohérent ni avec les limites à l'infini, ni avec les variations de la fonction
, car ce que « l'on voit » n'est cohérent ni avec les limites à l'infini, ni avec les variations de la fonction 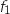 et par conséquent
et par conséquent 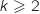 .
.
2.a Démontrer que pour 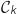 ne peut pas être la courbe représentative de
ne peut pas être la courbe représentative de 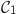 , car ce que « l'on voit » n'est cohérent ni avec les limites à l'infini, ni avec les variations de la fonction
, car ce que « l'on voit » n'est cohérent ni avec les limites à l'infini, ni avec les variations de la fonction 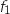 et par conséquent
et par conséquent 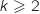 .
.
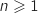 , toutes les courbes
, toutes les courbes 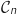 passent par le point O et un autre point dont on donnera les coordonnées.
passent par le point O et un autre point dont on donnera les coordonnées.
On a pour tout entier 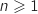 :
: 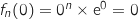 , donc toutes les courbes
, donc toutes les courbes 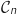 passent par O.
Par observation du dessin, on conjecture que le deuxième point commun est d'abscisse 1 et on calcule :
passent par O.
Par observation du dessin, on conjecture que le deuxième point commun est d'abscisse 1 et on calcule :
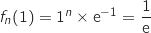 Donc toutes les courbes
Donc toutes les courbes 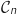 passent également par le point de coordonnées
passent également par le point de coordonnées 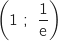 .
.
b. Vérifier que pour tout entier naturel 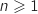 :
: 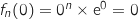 , donc toutes les courbes
, donc toutes les courbes 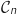 passent par O.
Par observation du dessin, on conjecture que le deuxième point commun est d'abscisse 1 et on calcule :
passent par O.
Par observation du dessin, on conjecture que le deuxième point commun est d'abscisse 1 et on calcule :
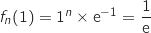 Donc toutes les courbes
Donc toutes les courbes 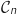 passent également par le point de coordonnées
passent également par le point de coordonnées 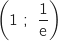 .
.
 supérieur ou égal à 2, et pour tout réel
supérieur ou égal à 2, et pour tout réel  ,
,
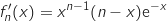
 semble admettre un maximum atteint pour
semble admettre un maximum atteint pour 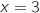 .
Valider cette conjecture à l'aide d'une démonstration.
.
Valider cette conjecture à l'aide d'une démonstration.
En utilisant l'expression générale de la dérivée trouvée dans la question 2.b. on a :
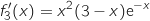
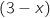 qui s'annule en changeant de signe.
Ainsi
qui s'annule en changeant de signe.
Ainsi 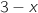 s'annule pour
s'annule pour 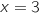 en changeant de signe avec :
en changeant de signe avec :
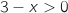 sur
sur 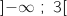 et
et 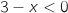 sur
sur 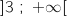 .
Cela justifie que
.
Cela justifie que 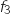 admet un maximum atteint pour
admet un maximum atteint pour 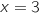 .
.
4.a Démontrer que la droite 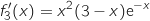
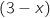 qui s'annule en changeant de signe.
Ainsi
qui s'annule en changeant de signe.
Ainsi 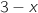 s'annule pour
s'annule pour 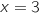 en changeant de signe avec :
en changeant de signe avec :
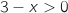 sur
sur 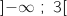 et
et 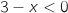 sur
sur 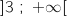 .
Cela justifie que
.
Cela justifie que 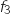 admet un maximum atteint pour
admet un maximum atteint pour 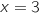 .
.
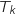 coupe l'axe des abscisses au point de coordonnées
coupe l'axe des abscisses au point de coordonnées 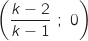 .
.
La droite 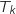 (
(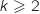 ) est tangente à la courbe
) est tangente à la courbe 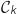 au point d'abscisse 1 donc son coefficient directeur est :
au point d'abscisse 1 donc son coefficient directeur est :
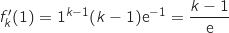 La droite
La droite 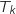 a donc une équation de la forme
a donc une équation de la forme 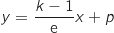 .
Pour déterminer
.
Pour déterminer 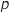 , on écrit que
, on écrit que 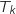 passe par le point de coordonnées
passe par le point de coordonnées 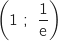 (voir question 2.a) et on obtient :
(voir question 2.a) et on obtient :
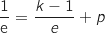 d'où
d'où 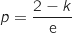 .
Donc l'équation réduite de
.
Donc l'équation réduite de 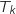 est
est 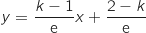 .
Pour trouver le point d'intersection avec l'axe des abscisses il reste à résoudre l'équation :
.
Pour trouver le point d'intersection avec l'axe des abscisses il reste à résoudre l'équation :
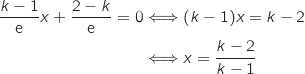 Donc la droite
Donc la droite 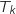 coupe l'axe des abscisses en
coupe l'axe des abscisses en 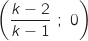 .
.
b. En déduire, à l'aide des données de l'énoncé, la valeur de l'entier 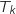 (
(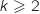 ) est tangente à la courbe
) est tangente à la courbe 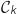 au point d'abscisse 1 donc son coefficient directeur est :
au point d'abscisse 1 donc son coefficient directeur est :
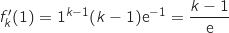 La droite
La droite 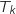 a donc une équation de la forme
a donc une équation de la forme 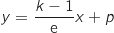 .
Pour déterminer
.
Pour déterminer 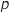 , on écrit que
, on écrit que 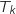 passe par le point de coordonnées
passe par le point de coordonnées 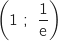 (voir question 2.a) et on obtient :
(voir question 2.a) et on obtient :
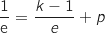 d'où
d'où 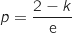 .
Donc l'équation réduite de
.
Donc l'équation réduite de 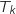 est
est 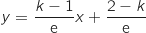 .
Pour trouver le point d'intersection avec l'axe des abscisses il reste à résoudre l'équation :
.
Pour trouver le point d'intersection avec l'axe des abscisses il reste à résoudre l'équation :
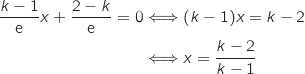 Donc la droite
Donc la droite 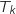 coupe l'axe des abscisses en
coupe l'axe des abscisses en 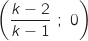 .
.
 .
.
On sait que A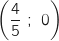 , donc pour
, donc pour 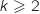 :
:
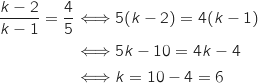
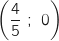 , donc pour
, donc pour 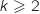 :
:
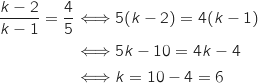
PARTIE B
On désigne par la suite définie pour tout entier
la suite définie pour tout entier  supérieur ou égal à 1 par
supérieur ou égal à 1 par
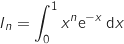
Dans le sujet original, la première question de la partie B nécessitait l'utilisation d'une intégration
par parties qui n'est plus au programme à compter de l'année scolaire 2012-2013.
2. Dans cette question, toute trace de recherche ou d'initiative, même incomplète, sera prise en compte dans l'évaluation.
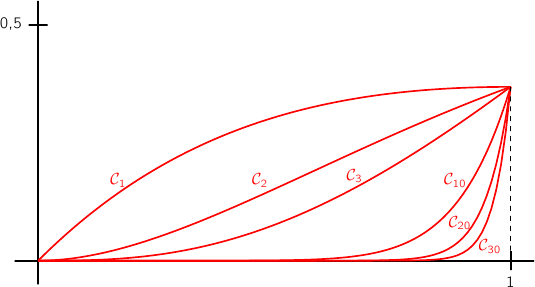
Sur le graphique ci-dessous, on a représenté les portions des courbes  comprises dans la bande définie par
comprises dans la bande définie par 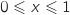 .
.
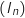 en décrivant la démarche.
en décrivant la démarche.
Pour tout 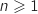 , sur l'intervalle
, sur l'intervalle  , les fonctions
, les fonctions 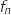 sont positives , donc l'intégrale
sont positives , donc l'intégrale 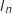 représente l'aire de la zone délimitée par la courbe
représente l'aire de la zone délimitée par la courbe 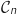 , l'axe des abscisses et la droite d'équation
, l'axe des abscisses et la droite d'équation  . Sur le dessin on voit que la zone est de plus en plus restreinte au fur et à mesure que
. Sur le dessin on voit que la zone est de plus en plus restreinte au fur et à mesure que  croît, donc on conjecture que la suite
croît, donc on conjecture que la suite 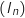 est décroissante.
est décroissante.
b. Démontrer cette conjecture.
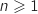 , sur l'intervalle
, sur l'intervalle  , les fonctions
, les fonctions 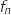 sont positives , donc l'intégrale
sont positives , donc l'intégrale 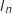 représente l'aire de la zone délimitée par la courbe
représente l'aire de la zone délimitée par la courbe 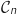 , l'axe des abscisses et la droite d'équation
, l'axe des abscisses et la droite d'équation  . Sur le dessin on voit que la zone est de plus en plus restreinte au fur et à mesure que
. Sur le dessin on voit que la zone est de plus en plus restreinte au fur et à mesure que  croît, donc on conjecture que la suite
croît, donc on conjecture que la suite 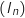 est décroissante.
est décroissante.
Pour tout entier 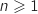 , on étudie le signe de
, on étudie le signe de 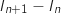 :
:
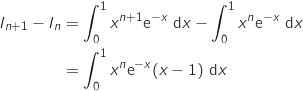 Pour
Pour 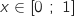 ,
, 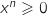 et
et 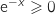 , parcontre
, parcontre 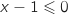 , donc la fonction à intégrer est négative sur l'intervalle considéré, ce qui entraîne que
l'intégrale est également négative, autrement dit on a :
Pour tout entier
, donc la fonction à intégrer est négative sur l'intervalle considéré, ce qui entraîne que
l'intégrale est également négative, autrement dit on a :
Pour tout entier 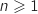 ,
, 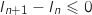 , ce qui prouve que la suite
, ce qui prouve que la suite 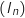 est décroissante.
est décroissante.
c. En déduire que la suite 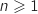 , on étudie le signe de
, on étudie le signe de 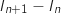 :
:
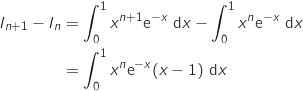 Pour
Pour 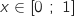 ,
, 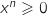 et
et 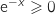 , parcontre
, parcontre 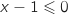 , donc la fonction à intégrer est négative sur l'intervalle considéré, ce qui entraîne que
l'intégrale est également négative, autrement dit on a :
Pour tout entier
, donc la fonction à intégrer est négative sur l'intervalle considéré, ce qui entraîne que
l'intégrale est également négative, autrement dit on a :
Pour tout entier 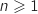 ,
, 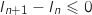 , ce qui prouve que la suite
, ce qui prouve que la suite 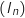 est décroissante.
est décroissante.
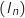 est convergente.
est convergente.
Tous les termes de la suite 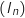 sont positifs puisque pour tout entier
sont positifs puisque pour tout entier 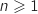 ,
, 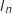 est l'intégrale sur
est l'intégrale sur  d'une fonction positive sur
d'une fonction positive sur  .
Ainsi la suite
.
Ainsi la suite 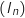 est décroissante et minorée par 0, donc elle est convergente.
est décroissante et minorée par 0, donc elle est convergente.
d. Déterminer 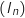 sont positifs puisque pour tout entier
sont positifs puisque pour tout entier 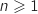 ,
, 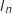 est l'intégrale sur
est l'intégrale sur  d'une fonction positive sur
d'une fonction positive sur  .
Ainsi la suite
.
Ainsi la suite 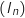 est décroissante et minorée par 0, donc elle est convergente.
est décroissante et minorée par 0, donc elle est convergente.
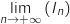 .
.
Sur  ,
, 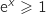 , donc
, donc 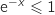 et
et 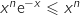 et du coup :
et du coup :
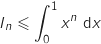 avec :
avec :
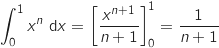 Ainsi
Ainsi 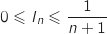 avec
avec 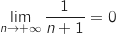 , donc d'après le théorème des gendarmes
, donc d'après le théorème des gendarmes 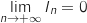 .
.
 ,
, 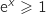 , donc
, donc 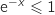 et
et 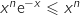 et du coup :
et du coup :
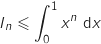 avec :
avec :
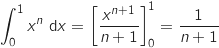 Ainsi
Ainsi 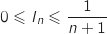 avec
avec 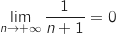 , donc d'après le théorème des gendarmes
, donc d'après le théorème des gendarmes 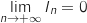 .
.
