Corrigé de l'exercice 4 de maths du bac S de juin 2011 en métropole
Cacher les corrigés
L'espace est muni d'un repère orthonormal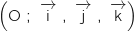
.
Bien que la notion de distance d'un point à un plan ne figure plus au programme, on peut quand même proposer cet exercice dans
la mesure où la partie A permet d'établir la formule qui sera utilisée par la suite dans l'exercice.
Il faut juste bien remarquer que la distance d'un point à un plan est la distance entre ce point et son projeté orthogonal sur le plan.
Partie A - Restitution organisée de connaissances
On désigne par
le plan d'équation 
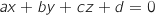et par 
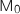le point de coordonnées 
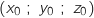. On appelle H le projeté orthogonal du point 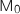sur le plan .
On suppose connue la propriété suivante :
Le vecteur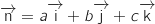 
est un vecteur normal au plan .
Le but de cette partie est de démontrer que la distance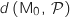 
du point 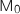au plan , c'est-à-dire la distance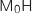 
, est telle que
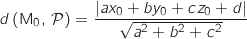
1. Justifier que
.
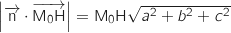2. Démontrer que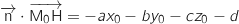 
.
3. Conclure.
Partie B
On désigne par A, B, C, F les points de coordonnées respectives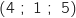
, 
.
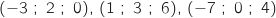1.a. Démontrer que les points A, B, C définissent un plan et que ce plan a pour équation cartésienne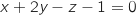 
.
b. Déterminer la distance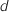 
du point F au plan .
On utilise directement la formule démontrée dans la partie A :
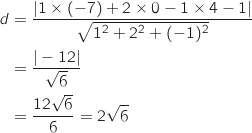
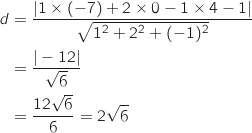
2. Le but de cette question est de calculer la distance
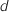par une autre méthode.
On appelle 
la droite qui passe par le point F et qui est perpendiculaire au plan .
a. Déterminer une représentation paramétrique de la droite .
Un vecteur normal de est 
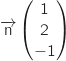(propriété rappelée dans la partie A).
Donc un vecteur directeur de est également 
, comme de plus passe par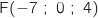 
, on a directement la représentation paramétrique de :
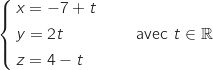
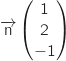b. Déterminer les coordonnées du point H, projeté orthogonal du point F sur le plan est (propriété rappelée dans la partie A).
Donc un vecteur directeur de est également , comme de plus passe par 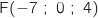, on a directement la représentation paramétrique de :
.
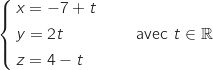
La droite est perpendiculaire à et passe par F, donc le projeté orthogonal de F sur est le point d'intersection entre et .
On trouve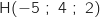 
.
c. Retrouver le résultat de la question 1. b.
est perpendiculaire à et passe par F, donc le projeté orthogonal de F sur est le point d'intersection entre et .
On trouve .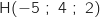
On calcule : 
.
On retrouve bien le résultat de la question 1.b.
3. Soit .
On retrouve bien le résultat de la question 1.b.
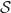la sphère de centre F et de rayon 6.
a. Justifier que le point B appartient à la sphère .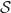
On calcule :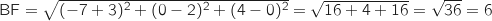 
.
Donc F appartient à la sphère .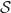
b. Préciser le centre et déterminer le rayon du cercle .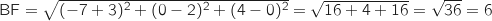
Donc F appartient à la sphère .
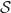, intersection de la sphère 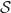et du plan .
est le cercle de centre H et de rayon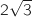 
.
