Corrigé de l'exercice 2 de maths du bac S d'avril 2012 à Pondichéry
Cacher les corrigés
Dans le repère orthonormé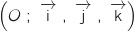
de l'espace, on considère :
- les plans
et 
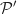d'équations :
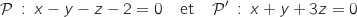
- la droite
ayant pour représentation paramétrique :
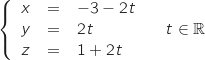
Proposition 1 La droite
est orthogonale au plan .
Un vecteur directeur de est 
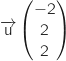(lecture directe sur la représentation paramétrique).
Un vecteur normal de est 
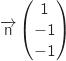(lecture directe sur l'équation cartésienne).
On remarque que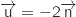 
, donc 
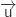et 
sont colinéaires ce qui justifie que la
droite est orthogonale au plan .
L'affirmation est VRAIE.
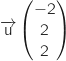est (lecture directe sur la représentation paramétrique).
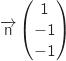Un vecteur normal de est (lecture directe sur l'équation cartésienne).
On remarque que 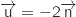, donc 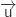et sont colinéaires ce qui justifie que la
droite est orthogonale au plan .
L'affirmation est VRAIE.
Dans le sujet original la question 2. porte sur des notions qui ne sont plus au programme à partir de la rentrée 2012.
Proposition 3 L'intersection des plans
et 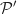est la droite 
dont une représentation paramétrique est :
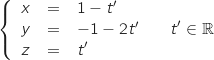
Les points de la droite sont de la forme 
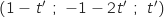avec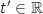 
, on regarde si ces coordonnées vérifient les équations des plans en question :
Plan : 
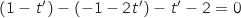pour tout
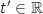Plan 
: 
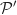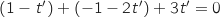pour tout
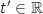Donc la droite est incluse dans et dans 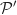, c'est donc la droite d'intersection des deux plans (les plans ne sont pas confondus, on peut le voir en vérifiant que O appartient à 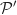, mais pas à ).
L'affirmation est VRAIE.
Proposition 4
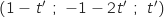Les droites sont de la forme avec 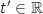, on regarde si ces coordonnées vérifient les équations des plans en question :
Plan : 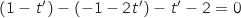pour tout
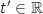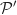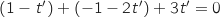Plan : pour tout
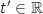Donc la droite est incluse dans et dans 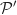, c'est donc la droite d'intersection des deux plans (les plans ne sont pas confondus, on peut le voir en vérifiant que O appartient à 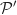, mais pas à ).
L'affirmation est VRAIE.
et sont coplanaires.
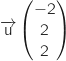Les vecteurs directeurs de et sont : et
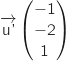, on remarque qu'ils ne sont pas colinéaires, donc les droites ne sont pas parallèles.
Pour savoir si les droites sont coplanaires, il reste à regarder si elles sont concourantes en résolvant :
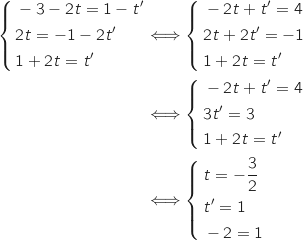Le système n'a pas de solution, donc les droites ne sont pas concourantes et comme elles ne sont pas parallèles on en déduit qu'elles sont non coplanaires.
L'affirmation est FAUSSE.
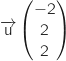et sont : et
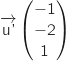, on remarque qu'ils ne sont pas colinéaires, donc les droites ne sont pas parallèles.
Pour savoir si les droites sont coplanaires, il reste à regarder si elles sont concourantes en résolvant :
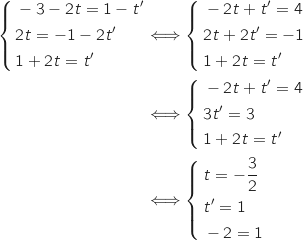Le système n'a pas de solution, donc les droites ne sont pas concourantes et comme elles ne sont pas parallèles on en déduit qu'elles sont non coplanaires.
L'affirmation est FAUSSE.
