Corrigé de l'exercice 4 du bac S de maths 2011 au Liban
Cacher les corrigés
Soit
la fonction définie sur 
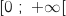par
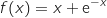
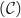la courbe représentative de dans un repère orthonormal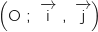 
Partie A
1. Etudier les variations de la fonction sur .
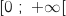La fonction est dérivable sur 
et on a :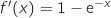 
.
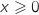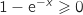Pour tout 
, 
et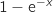 
ne s'annule que pour 
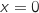, donc
la fonction est strictement croissante sur l'intervalle considéré.
2. Déterminer la limite de est dérivable sur et on a : .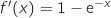
Pour tou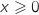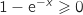t , et 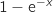ne s'annule que pour 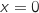, donc
la fonction est strictement croissante sur l'intervalle considéré.
en 
.
.
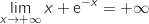Dans l'exercice original, la dernière question de cette partie portait sur la notion d'asymptote oblique qui n'est
plus au programme à partir de la session 2013 du baccalauréat.
Partie B
On considère la suite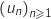
à termes positifs définie par :
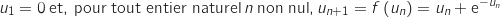
positif,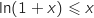 
.
On pourra étudier la fonction 
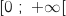définie sur par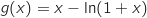 
.
Pour étudier les variations de , on calcule la dérivée de la fonction, on obtient :
.
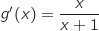Comme 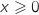, on a directement le signe de 
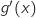et le tableau de variations :
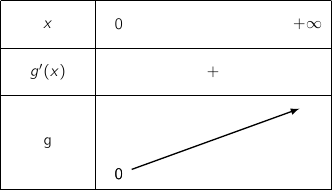
On remarque que sur , la fonction adment pour minimum 0, donc pour tout
, 
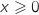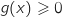, soit 
.
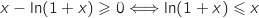, on calcule la dérivée de la fonction, on obtient :
.
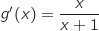Comme 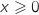, on a directement le signe de 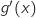et le tableau de variations :
, la fonction adment pour minimum 0, donc pour tout
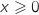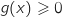, , soit .
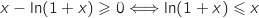2. En déduire que, pour tout entier naturel
non nul,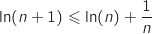 
.
En utilisant l'inégalité prouvée dans la question 1, avec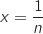 
, on obtient :
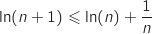
3. Démontrer que, pour tout entier naturel 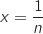, on obtient :
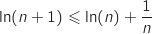
non nul, 
.
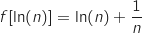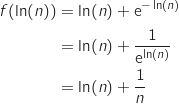
non nul,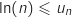 
.
Initialisation au rang 1
On a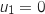 
et 
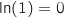, donc 
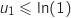Hérédité
On suppose que pour un entier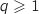 
, on a 
.
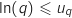On applique la fonction , croissante sur à cette inégalité :
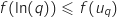Or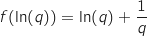 
(question 3) et 
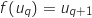, on a donc :
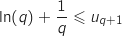En utilisant l'inégalité de la question 2. il vient :
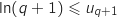Donc la propriété est héréditaire et comme elle est initialisée au rang 1, on peut dire qu'elle est vraie pour tout entier
supérieur ou égal à 1.
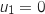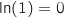5. En déduire la limite de la suite et , donc
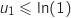Hérédité
On suppose que pour un entier 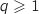, on a .
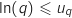On applique la fonction , croissante sur à cette inégalité :
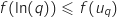Or 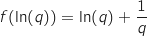(question 3) et 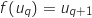, on a donc :
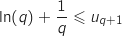En utilisant l'inégalité de la question 2. il vient :
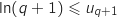Donc la propriété est héréditaire et comme elle est initialisée au rang 1, on peut dire qu'elle est vraie pour tout entier
supérieur ou égal à 1.
·
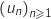D'après la question précédente :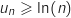 
, or 
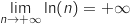, donc par comparaison, 
.
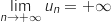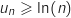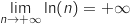Dans la suite de l'exercice, on admet que, pour tout entier , or , donc par comparaison, .
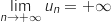supérieur ou égal à 
.
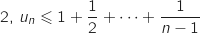6.a. Démontrer que, pour tout entier 
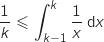
supérieur ou égal à 2, on a :
supérieur ou égal à 2, on a :
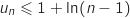
a. On remarque que sur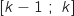 
, 
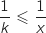, en intégrant on obtient l'inégalité demandée.
b. Dans l'inégalité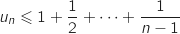 
, on majore chaque fraction avec une intégrale en utilisant le a. et avec la relation de Chasles on obtient :
.
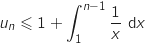
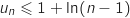7. Pour tout entier 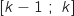, , 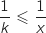en intégrant on obtient l'inégalité demandée.
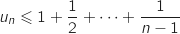b. Dans l'inégalité , on majore chaque fraction avec une intégrale en utilisant le a. et avec la relation de Chasles on obtient :
.
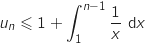
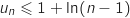supérieur ou égal à 2, on a montré que
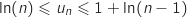
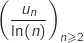converge vers 1.
Pour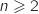 
, en divisant l'inégalité par 
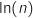et en utilisant le théorème des gendarmes, on montre qu'effectivement la suite converge vers 1.
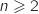, en divisant l'inégalité par 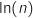et en utilisant le théorème des gendarmes, on montre qu'effectivement la suite converge vers 1.
