Corrigé de l'exercice 1 du bac S de maths 2011 en Nouvelle-Calédonie
Cacher les corrigés
Partie A : Restitution organisée de connaissances
Dans le sujet original, cette partie était consacrée aux équations différentielles qui ne sont plus au programme
à partir de la session 2013.
Partie B
Cette partie a été modifiée pour être conforme au nouveau programme en vigueur pour la session 2013.
Un cycliste roule sur une route descendante rectiligne et très longue. On note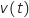 
sa vitesse à l'instant 
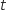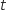, où est exprimé en secondes et 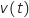en mètres par seconde.
On suppose que, lorsque le cycliste s'élance, sa vitesse initiale est nulle, c'est-à-dire que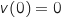 
.
On suppose de plus que la fonction 
ainsi définie est dérivable sur l'intervalle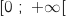 
.
Un modèle simple permet de considérer que la fonction est définie par :
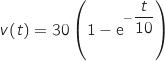
1.a. Déterminer le sens de variation de la fonction
sur l'intervalle .
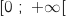La fonction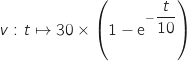 
est définie et dérivable sur 
.
La fonction 
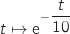est de la forme 
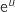avec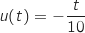 
, donc sa dérivée
est de la forme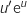 
, ce qui donne 
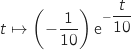La dérivée de la fonction constante 1 est nulle.
Finalement, on a :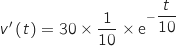 
, soit 
.
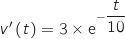Il est clair que la dérivée est strictement positive sur , donc la fonction est strictement
croissante sur cet intervalle.
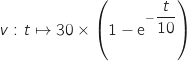est définie et dérivable sur .
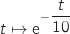La fonction est de la forme 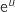avec 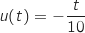, donc sa dérivée
est de la forme 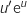, ce qui donne
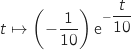La dérivée de la fonction constante 1 est nulle.
Finalement, on a : 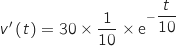, soit .
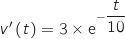Il est clair que la dérivée est strictement positive sur , donc la fonction est strictement
croissante sur cet intervalle.
b. Déterminer la limite de la fonction
en 
.
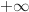Limite de la fonction en 
:
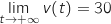
2. On considère, dans cette situation, que la vitesse du cycliste est stabilisée lorsque son accélération en :
-
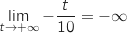(limite de référence)
- Par composition :
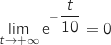
- Par addition :
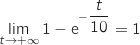
- Par produit :
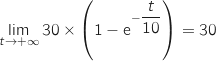
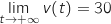
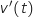est inférieure à 0,1 m.s
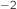. Déterminer, à la seconde près, la plus petite valeur de 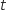à partir de laquelle la vitesse du cycliste est stabilisée.
On a déjà vu que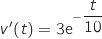 
, on résout l'inéquation :
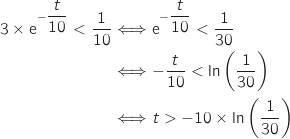Avec : 
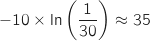secondes.
3. La distance 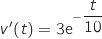, on résout l'inéquation :
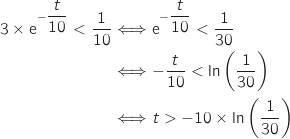Avec : 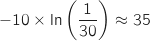secondes.
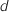parcourue par ce cycliste entre les instants 
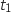, et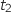 
est donnée par 
.
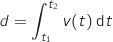Calculer la distance parcourue par ce cycliste pendant les 35 premières secondes.
On commence par déterminer un primitive de la fonction , définie et continue sur par :
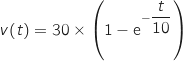On écrit 
.
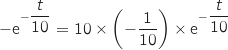La fonction 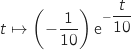est de la forme 
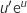, donc une primitive est 
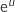c'est à dire :
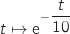Par conséquent une primitive de 
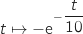est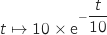 
.
Une primitive de la fonction constante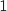 
est la fonction 
.
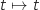Finalement une primitive de est la fonction définie par :
.
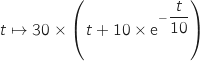Avec la primitive trouvée on peut maintenant calculer l'intégrale :
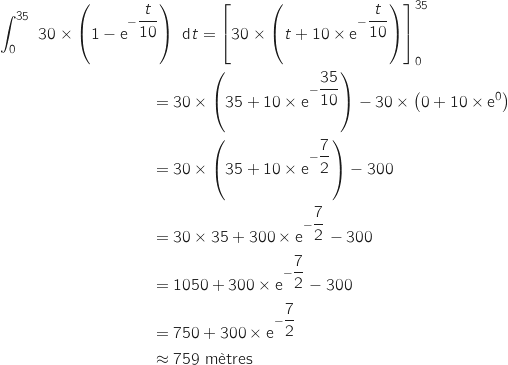
, définie et continue sur par :
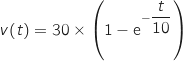On écrit .
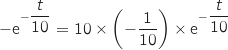La fonction 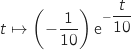est de la forme 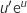, donc une primitive est 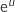c'est à dire :
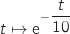Par conséquent une primitive de 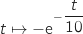est .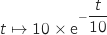
Une primitive de la fonction constante 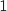est la fonction .
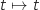Finalement une primitive de est la fonction définie par :
.
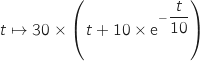Avec la primitive trouvée on peut maintenant calculer l'intégrale :
