Correction de l'exercice 3 du bac S 2011 de maths en Nouvelle-Calédonie
Cacher les corrigés
Soit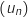 la suite définie pour tout entier naturel
la suite définie pour tout entier naturel  par :
par :
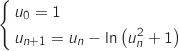
Partie A
Soit la fonction définie sur
la fonction définie sur 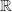 par
par
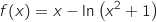
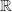 l'équation
l'équation 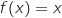 .
.
On résout l'équation :
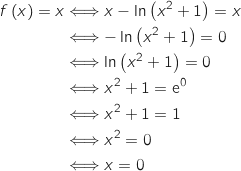
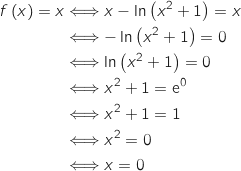
2. Étudier le sens de variation de la fonction
 sur l'intervalle
sur l'intervalle  .
En déduire que si
.
En déduire que si 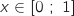 alors
alors 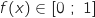 .
.
La fonction 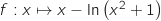 est définie et dérivable sur
est définie et dérivable sur  .
La fonction
.
La fonction 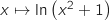 est de la forme
est de la forme 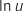 avec
avec 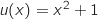 ,
donc sa dérivée est de la forme
,
donc sa dérivée est de la forme 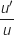 ,
ce qui donne
,
ce qui donne 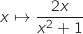 Donc
Donc 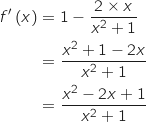 Le signe de la dérivée est le même que celui de
Le signe de la dérivée est le même que celui de 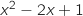 .
On remarque que
.
On remarque que 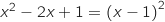 Donc la dérivée est positive sur
Donc la dérivée est positive sur  et la fonction
et la fonction  est croissante sur cet intervalle.
On a le tableau de variations :
est croissante sur cet intervalle.
On a le tableau de variations :
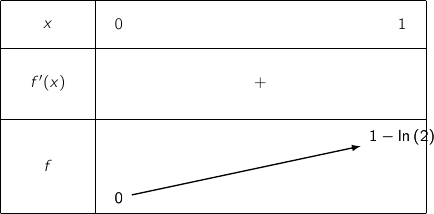
Avec 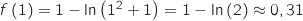 .
D'après le tableau de variations, pour tout
.
D'après le tableau de variations, pour tout 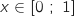 ,
, 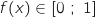 .
.
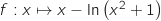 est définie et dérivable sur
est définie et dérivable sur  .
La fonction
.
La fonction 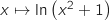 est de la forme
est de la forme 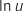 avec
avec 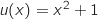 ,
donc sa dérivée est de la forme
,
donc sa dérivée est de la forme 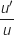 ,
ce qui donne
,
ce qui donne 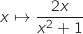 Donc
Donc 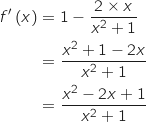 Le signe de la dérivée est le même que celui de
Le signe de la dérivée est le même que celui de 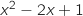 .
On remarque que
.
On remarque que 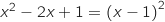 Donc la dérivée est positive sur
Donc la dérivée est positive sur  et la fonction
et la fonction  est croissante sur cet intervalle.
On a le tableau de variations :
est croissante sur cet intervalle.
On a le tableau de variations :

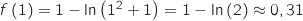 .
D'après le tableau de variations, pour tout
.
D'après le tableau de variations, pour tout 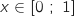 ,
, 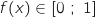 .
.
Partie B
1. Démontrer par récurrence que, pour tout entier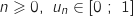 .
.
La propriété à montrer pour tout entier 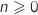 est :
est :
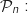 «
«
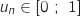 ».
Initialisation
».
Initialisation
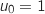 Donc
Donc 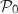 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 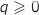 , on a donc l'hypothèse de récurrence :
, on a donc l'hypothèse de récurrence :
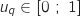 On montre qu'alors la propriété est vraie au rang
On montre qu'alors la propriété est vraie au rang 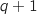 .
D'après l'hypothèse de récurrence :
.
D'après l'hypothèse de récurrence : 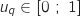 et d'après la partie A,
et d'après la partie A,
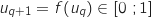 .
Donc
.
Donc  est vraie.
Ainsi la propriété est vraie au rang
est vraie.
Ainsi la propriété est vraie au rang 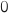 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier
et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier 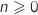 .
.
2. Étudier le sens de variation de la suite 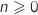 est :
est :
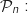 «
«
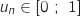 ».
Initialisation
».
Initialisation
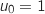 Donc
Donc 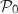 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 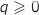 , on a donc l'hypothèse de récurrence :
, on a donc l'hypothèse de récurrence :
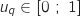 On montre qu'alors la propriété est vraie au rang
On montre qu'alors la propriété est vraie au rang 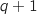 .
D'après l'hypothèse de récurrence :
.
D'après l'hypothèse de récurrence : 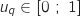 et d'après la partie A,
et d'après la partie A,
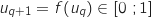 .
Donc
.
Donc  est vraie.
Ainsi la propriété est vraie au rang
est vraie.
Ainsi la propriété est vraie au rang 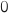 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier
et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier 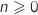 .
.
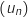 .
.
En utilisant la relation de récurrence de la suite on a :
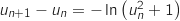 Comme
Comme 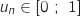 ,
, 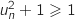 , donc
, donc 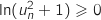 et
et 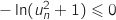 ,
donc la suite est décroissante.
,
donc la suite est décroissante.
3. Démontrer que la suite 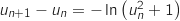 Comme
Comme 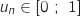 ,
, 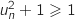 , donc
, donc 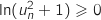 et
et 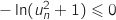 ,
donc la suite est décroissante.
,
donc la suite est décroissante.
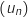 est convergente.
On admet que la limite
est convergente.
On admet que la limite 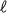 de
de  est solution de l'équation
est solution de l'équation 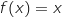 .
Déterminer
.
Déterminer 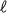 .
.
La suite en question est décroissante et minorée par 0, donc elle est convergente.
La limite de la suite est solution de l'équation 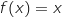 et comme cette équation n'a qu'une solution qui vaut 0 (voir
partie A), on en conclut que
et comme cette équation n'a qu'une solution qui vaut 0 (voir
partie A), on en conclut que 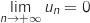 .
.
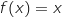 et comme cette équation n'a qu'une solution qui vaut 0 (voir
partie A), on en conclut que
et comme cette équation n'a qu'une solution qui vaut 0 (voir
partie A), on en conclut que 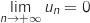 .
.
