Corrigé de l'exercice 1 du bac S de maths 2011 à Pondichéry
Cacher les corrigés
Partie I
Sur le graphique ci-dessous, on a représenté dans un repère orthonormal, les courbes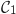 et
et 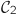 représentatives de deux fonctions
représentatives de deux fonctions 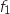 et
et 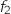 définies sur l'intervalle
définies sur l'intervalle  .
.
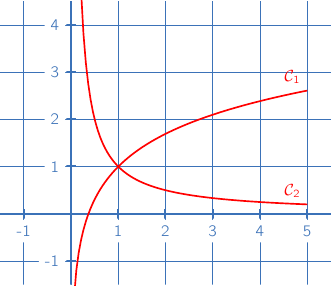
- l'axe des ordonnées est asymptote aux courbes
 et
et  .
.
- l'axe des abscisses est asymptote à la courbe
 .
.
- la fonction
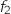 est continue et strictement décroissante sur l'intervalle
est continue et strictement décroissante sur l'intervalle  .
.
- la fonction
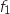 est continue et strictement croissante sur l'intervalle
est continue et strictement croissante sur l'intervalle  .
.
- la limite quand
 tend vers
tend vers  de
de 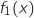 est
est  .
.
Pour chacune des quatre questions de cette partie, une seule des trois propositions est exacte. Le candidat indiquera sur la copie la réponse choisie. Aucune justification n'est demandée. Chaque réponse juste rapporte 0,5 point. Une réponse fausse ou l'absence de réponse n'est pas sanctionnée. 1. La limite quand
 tend vers 0 de
tend vers 0 de 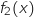 est :
est :

La bonne réponse est  .
.
2. La limite quand  .
.
 tend vers
tend vers  de
de 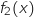 est :
est :

La bonne réponse est 0.
Dans le sujet orignal la question 3. porte sur une notion désormais hors programme.
4. Le tableau de signes de
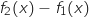 est :
est :
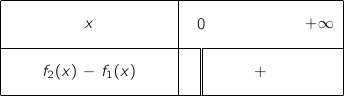
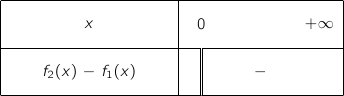
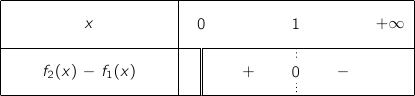
Le bon tableau est le dernier proposé.
Partie II
On considère la fonction définie sur l'intervalle
définie sur l'intervalle  par
par
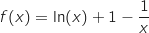
 aux bornes de son ensemble de définition.
aux bornes de son ensemble de définition.
Limite à droite en 0 :
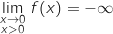 Limite en
Limite en  :
:
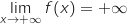
2. Etudier les variations de la fonction -
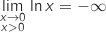 (limite de référence)
(limite de référence)
-
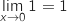 (limite d'une constante)
(limite d'une constante)
-
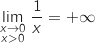 (limite de référence) et par produit par
(limite de référence) et par produit par 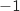 on obtient :
on obtient : 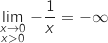
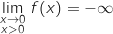 Limite en
Limite en  :
:
-
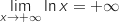 (limite de référence)
(limite de référence)
-
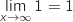 (limite d'une constante)
(limite d'une constante)
-
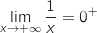 (limite de référence) et par produit par
(limite de référence) et par produit par 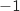 on obtient :
on obtient : 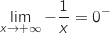
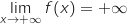
 sur l'intervalle
sur l'intervalle  .
.
Sur 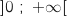 , la fonction
, la fonction 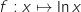 est croissante, la fonction
est croissante, la fonction 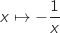 est croissante donc par addition la fonction
est croissante donc par addition la fonction  est croissante.
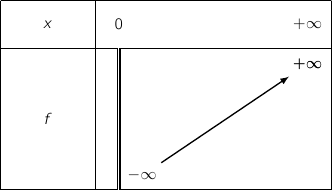
On a donc le tableau de variations :
est croissante.
On a donc le tableau de variations :
3. En déduire le signe de 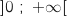 , la fonction
, la fonction 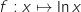 est croissante, la fonction
est croissante, la fonction 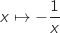 est croissante donc par addition la fonction
est croissante donc par addition la fonction  est croissante.
On a donc le tableau de variations :
est croissante.
On a donc le tableau de variations :

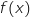 lorsque
lorsque  décrit l'intervalle
décrit l'intervalle  .
.
On remarque que 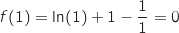 , compte tenu des variations de
, compte tenu des variations de  on a le tableau de signes :
on a le tableau de signes :

4. Montrer que la fonction 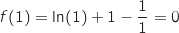 , compte tenu des variations de
, compte tenu des variations de  on a le tableau de signes :
on a le tableau de signes :

 définie sur l'intervalle
définie sur l'intervalle  par
par
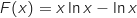
 sur cet intervalle.
sur cet intervalle.
On dérive la fonction  :
:
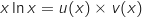 avec :
avec : 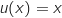
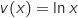 Les fonctions
Les fonctions  et
et  sont dérivables sur
sont dérivables sur 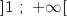 , donc
, donc 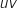 est également dérivable sur cet intervalle et on a :
est également dérivable sur cet intervalle et on a :
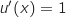
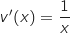
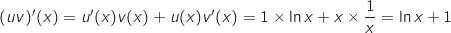 Donc
Donc 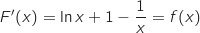 , ce qui prouve que
, ce qui prouve que  est une primitive de
est une primitive de  sur
sur 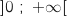 .
.
5. Démontrer que la fonction  :
:
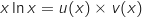 avec :
avec : 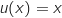
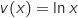 Les fonctions
Les fonctions  et
et  sont dérivables sur
sont dérivables sur 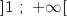 , donc
, donc 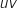 est également dérivable sur cet intervalle et on a :
est également dérivable sur cet intervalle et on a :
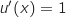
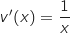
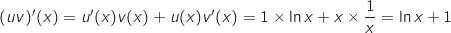 Donc
Donc 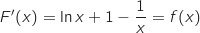 , ce qui prouve que
, ce qui prouve que  est une primitive de
est une primitive de  sur
sur 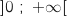 .
.
 est strictement croissante sur l'intervalle
est strictement croissante sur l'intervalle 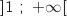 .
.
On étudie le signe de 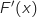 sur
sur 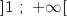 :
Comme
:
Comme  est une primitive de
est une primitive de  ,
, 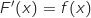 , d'après ce qui précède on a
, d'après ce qui précède on a 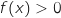 sur
sur 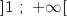 , donc
, donc
 est strictement croissante sur
est strictement croissante sur 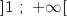 .
.
6. Montrer que l'équation 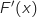 sur
sur 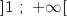 :
Comme
:
Comme  est une primitive de
est une primitive de  ,
, 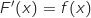 , d'après ce qui précède on a
, d'après ce qui précède on a 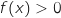 sur
sur 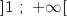 , donc
, donc
 est strictement croissante sur
est strictement croissante sur 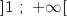 .
.
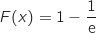 admet une unique solution dans l'intervalle
admet une unique solution dans l'intervalle 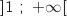 qu'on
note
qu'on
note  .
.
La fonction  est continue sur
est continue sur 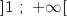 et d'après le tableau de variations, l'image de cet intervalle par
et d'après le tableau de variations, l'image de cet intervalle par  est l'intervalle
est l'intervalle 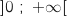 , or
, or 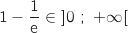 donc d'après le théorème des valeurs intermédiaires l'équation
donc d'après le théorème des valeurs intermédiaires l'équation 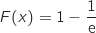 admet au moins une solution dans
admet au moins une solution dans 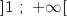 .
Comme de plus la fonction est strictement croissante sur l'intervalle considéré, la solution est unique.
.
Comme de plus la fonction est strictement croissante sur l'intervalle considéré, la solution est unique.
7. Donner un encadrement de  est continue sur
est continue sur 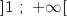 et d'après le tableau de variations, l'image de cet intervalle par
et d'après le tableau de variations, l'image de cet intervalle par  est l'intervalle
est l'intervalle 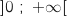 , or
, or 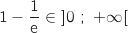 donc d'après le théorème des valeurs intermédiaires l'équation
donc d'après le théorème des valeurs intermédiaires l'équation 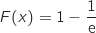 admet au moins une solution dans
admet au moins une solution dans 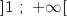 .
Comme de plus la fonction est strictement croissante sur l'intervalle considéré, la solution est unique.
.
Comme de plus la fonction est strictement croissante sur l'intervalle considéré, la solution est unique.
 d'amplitude
d'amplitude 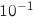 .
.
En utilisant la technique de balayage avec la calculette on trouve 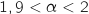 .
.
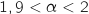 .
.
Partie III
Soit et
et 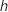 les fonctions définies sur l'intervalle
les fonctions définies sur l'intervalle 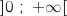 par :
par :
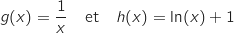
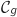 et
et 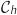 représentatives des fonctions
représentatives des fonctions  et
et 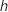 .
.
 et de l'axe des abscisses. Déterminer les coordonnées du point A.
et de l'axe des abscisses. Déterminer les coordonnées du point A.
Pour trouver l'abscisse de A on résout :
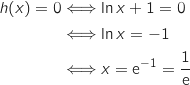 Donc A
Donc A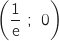 .
.
2. P est le point d'intersection des courbes 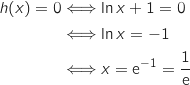 Donc A
Donc A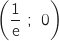 .
.
 et
et 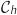 . Justifier que les coordonnées du point P sont (1 ; 1).
. Justifier que les coordonnées du point P sont (1 ; 1).
Pour trouver l'abscisse du point P, on résout :
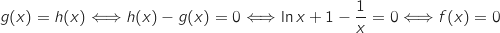 .
Compte tenu du signe de
.
Compte tenu du signe de  vu dans la question 3 de la partie II, cette équation a une unique solution sur
vu dans la question 3 de la partie II, cette équation a une unique solution sur  qui est
qui est  .
On vérifie que :
.
On vérifie que : 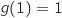 et que
et que 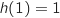 , donc P
, donc P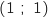 est bien le point d'intersection de
est bien le point d'intersection de  et
et  .
.
3. On note 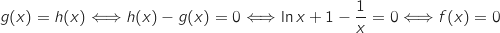 .
Compte tenu du signe de
.
Compte tenu du signe de  vu dans la question 3 de la partie II, cette équation a une unique solution sur
vu dans la question 3 de la partie II, cette équation a une unique solution sur  qui est
qui est  .
On vérifie que :
.
On vérifie que : 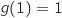 et que
et que 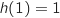 , donc P
, donc P est bien le point d'intersection de
est bien le point d'intersection de 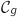 et
et 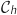 .
.
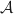 l'aire du domaine délimité par les courbes
l'aire du domaine délimité par les courbes 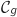 ,
, 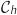 et les droites d'équations respectives
et les droites d'équations respectives
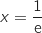 et
et 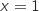 (domaine grisé sur le graphique).
a. Exprimer l'aire
(domaine grisé sur le graphique).
a. Exprimer l'aire 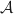 à l'aide de la fonction
à l'aide de la fonction  définie dans la partie II.
définie dans la partie II.
On remarque que 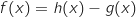 , donc sur
, donc sur 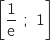 ,
, 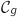 est au dessus de
est au dessus de 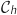 (voir le signe de
(voir le signe de  dans la partie II), et l'aire grisée
s'obtient en calculant :
dans la partie II), et l'aire grisée
s'obtient en calculant :
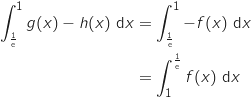
b. Montrer que 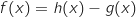 , donc sur
, donc sur 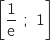 ,
, 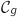 est au dessus de
est au dessus de 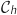 (voir le signe de
(voir le signe de  dans la partie II), et l'aire grisée
s'obtient en calculant :
dans la partie II), et l'aire grisée
s'obtient en calculant :
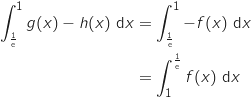
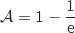 .
.
Dans la partie II, on a vu qu'une primitive de  sur
sur  est définie par
est définie par 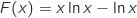 , donc :
, donc :
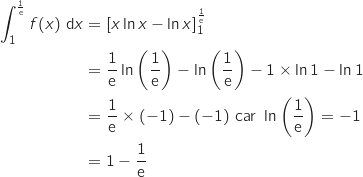
4. Soit  sur
sur  est définie par
est définie par 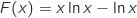 , donc :
, donc :
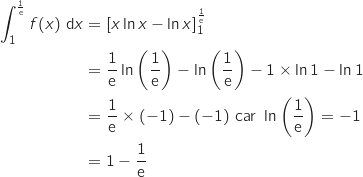
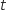 un nombre réel de l'intervalle
un nombre réel de l'intervalle 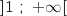 . On note
. On note 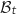 l'aire du domaine délimité par les droites d'équations respectives
l'aire du domaine délimité par les droites d'équations respectives 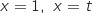 et les courbes
et les courbes 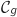 et
et 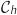 (domaine hachuré sur le graphique).
On souhaite déterminer une valeur de
(domaine hachuré sur le graphique).
On souhaite déterminer une valeur de 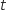 telle que
telle que 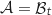 .
a. Montrer que
.
a. Montrer que 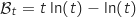 .
.
Pour 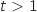 , sur
, sur 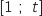 ,
, 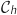 est au dessus de
est au dessus de 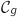 (toujours en remarquant que
(toujours en remarquant que 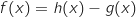 et avec le signe de la partie II), donc l'aire
hachurée est donnée par :
et avec le signe de la partie II), donc l'aire
hachurée est donnée par :
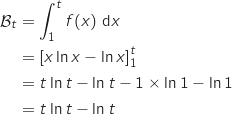
b. Conclure.
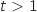 , sur
, sur 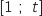 ,
, 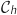 est au dessus de
est au dessus de 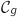 (toujours en remarquant que
(toujours en remarquant que 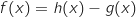 et avec le signe de la partie II), donc l'aire
hachurée est donnée par :
et avec le signe de la partie II), donc l'aire
hachurée est donnée par :
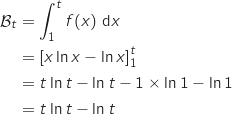
Pour trouver  tel que
tel que 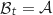 , on résout l'équation :
, on résout l'équation :
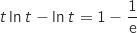 soit
soit 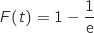 .
On a vu dans la partie II que cette équation a une unique solution
.
On a vu dans la partie II que cette équation a une unique solution  , donc
, donc 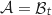 équivaut à
équivaut à 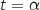 .
.
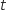 tel que
tel que 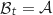 , on résout l'équation :
, on résout l'équation :
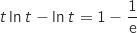 soit
soit 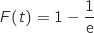 .
On a vu dans la partie II que cette équation a une unique solution
.
On a vu dans la partie II que cette équation a une unique solution  , donc
, donc 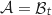 équivaut à
équivaut à 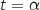 .
.
