Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2015 en Amérique du nord
Cacher les corrigés
Dans l'espace, on considère une pyramide SABCE à base carrée ABCE de centre O.
Soit D le point de l'espace tel que soit un repère orthonormé.
Le point S a pour coordonnées dans ce repère.
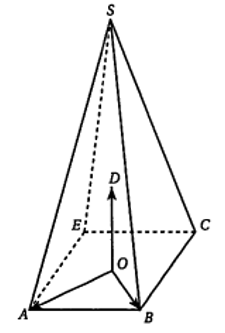
Partie A
1. Soit U le point de la droite (SB) de cote 1. Construire le point U sur la figure.
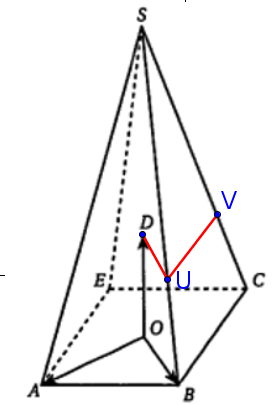
2. Soit V le point d'intersection du plan (AEU) et de la droite (SC). Montrer que les droites (UV) et (BC) sont parallèles.
Construire le point V sur la figure.
Compte tenu de la configuration les plans (AEU) et (SBC) sont sécants selon la droite (UV). (Les points U et V appartiennent aux deux plans sécants considérés).
Dans le plan (AEU) nous avons la droite (EA).
Dans le plan (SBC) nous avons la droite (BC).
Comme ABCE est un carré les droites (EA) et (BC) sont parallèles.
Donc d'après le théorème du toit la droite d'intersection (UV) des deux plans est parallèles à (EA) et à (BC).
3. Soit K le point de coordonnées .
Montrer que K est le pied de la hauteur issue de U dans le trapèze AUVE.
Dans le triangle SOB, nous avons (DU) qui est parallèle à (OB).
Comme S a pour coordonnées , nous avons : .
En utilisant la propriété de Thalès dans le triangle SOB nous obtenons :
, du coup l'ordonnée de U est .
Finalement .
Nous avons et donc
soit
Nous avons et donc :
soit
En utilisant la relation du produit scalaire en repère orthonormé :
Cela montre que et sont orthogonaux.
Il reste à montre que K appartient à (EA).
Nous avons : soit
Du coup , ce qui montre que les vecteurs considérés sont colinéaires et donc que K est un point de la droite (EA).
Ainsi K appartient à (EA) et (UK) est perpendiculaire à (EA) donc K est le pied de la hauteur issue de U dans le trapèze AUVE.
Partie B
Dans cette partie, on admet que l'aire du quadrilatère AUVE est .
1. On admet que le point U a pour coordonnées .
Vérifier que le plan (EAU) a pour équation .
On vérifie que les points E, A et U appartiennent au plan dont une équation cartésienne nous est donnée.
Pour : .
Pour :
Pour :
Ainsi les 3 points considérés appartiennent au plan d'équation cartésienne , l'équation en question est donc une équation de (EAU).
2. Donner une représentation paramétrique de la droite orthogonale au plan (EAU) passant par le point S.
Par lecture sur l'équation donnée à la question 1, nous obtenons un vecteur normal au plan (EAU) :
La droite admet comme vecteur directeur et une représentation paramétrique est :
3. Déterminer les coordonnées de H, point d'intersection de la droite et du plan (EAU).
Nous résolvons le système :
Donc
4. Le plan (EAU) partage la pyramide (SABCE) en deux solides. Ces deux solides ont-ils le même volume ?
On calcule déjà le volume de la pyramide SABCE à base carrée ABCE et de hauteur [OS] :
On notera que le côté du carré ABCE est de la longueur de la diagonale d'un carré de côté 1, donc vaut .
Le plan (EAU) partage la pyramide (SABCE) en deux solides, un de ces deux solides est la pyramide de sommet S dont la base est le trapèze AUVE, et dont la hauteur est [SH].
On calcule maintenant le volume de cette pyramide :
Avec
Donc .
Comme , on conclut que la pyramide n'est pas partagée en deux solides de même volume.
