Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2015 en Amérique du nord
Cacher les corrigés
On se place dans un repère orthonormé et, pour tout entier naturel , on définit les points par leurs coordonnées de la façon suivante :
et pour tout entier naturel :
1.a. Déterminer les coordonnées des points , et .
Donc
Donc
b. Pour construire les points ainsi obtenus, on écrit l'algorithme suivant :
| Variables : | , , et sont des nombres réels |
| Initialisation : | prend la valeur |
| prend la valeur 4 | |
| Traitement : | Pour allant de 0 à 20 |
| Construire le point de coordonnées | |
| prend la valeur | |
| prend la valeur ...... | |
| prend la valeur ...... | |
| Fin pour |
Recopier et compléter cet algorithme pour qu'il construise les points à .
| Variables : | , , et sont des nombres réels |
| Initialisation : | prend la valeur |
| prend la valeur 4 | |
| Traitement : | Pour allant de 0 à 20 |
| Construire le point de coordonnées | |
| prend la valeur | |
| prend la valeur | |
| prend la valeur | |
| Fin pour |
c. A l'aide d'un tableur, on a obtenu le nuage de points suivant :
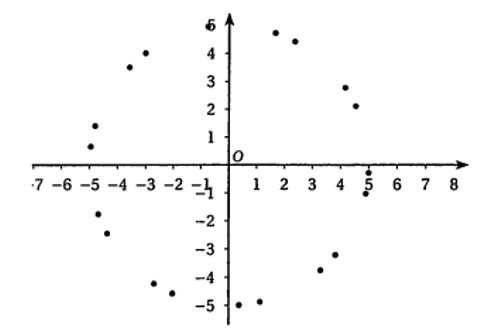
Identifier les points , et . On les nommera sur la figure.
Quel semble être l'ensemble auquel appartient les points pour tout entier naturel ?
Les points semblent appartenir au cercle de centre O et de rayon 5.
Voir la figure en fin de corrigé.
2. Le but de cette question est de construire géométriquement les points pour tout entier naturel.
Dans le plan complexe, on nomme, pour tout entier naturel , l'affixe du point .
a. Soit . Montrer que, pour tout entier naturel , .
Quelle interprétation géométrique peut-on faire de ce résultat ?
On effectue la démonstration par récurrence.
La propriété à montrer pour tout entier naturel est :
: « »
Initialisation au rang 0
Nous avons
et
Donc est vraie.
Hérédité
On suppose que pour un entier naturel : (hypothèse de récurrence).
Montrons qu'alors .
Du coup la propriété est héréditaire.
Ainsi la propriété considérée est vraie au rang 0 et elle est héréditaire, donc pour tout entier naturel : .
Cela montre que tous les points d'affixe , c'est à dire les points sont sur le cercle de centre O et de rayon 5.
b. On admet qu'il existe un réel tel que et .
Montrer que, pour tout entier naturel , .
Pour tout entier naturel :
c. Démontrer que, pour tout entier naturel , .
On fait de nouveau une démonstration par récurrence. Cette fois la propriété à montrer pour tout entier naturel est :
: « »
Initialisation au rang 0
Donc est vraie.
Hérédité
On suppose que pour un entier naturel : (hypothèse de récurrence).
On chercher à montrer qu'alors :
En partant de l'hypothèse de récurrence :
En multipliant par on obtient :
Donc la propriété est héréditaire.
Du coup la propriété est vraie au rang 0 et est héréditaire donc pour tout entier naturel : .
d. Montrer que est un argument du nombre complexe .
; et on écrit :
Un argument de est tel que :
D'autre part on a les relations d'angles associés :
Du coup on peut prendre pour un argument de .
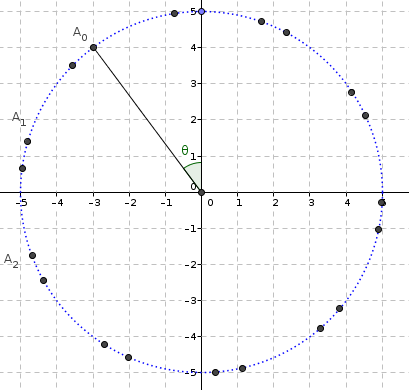
e. Pour tout entier naturel , déterminer, en fonction de et , un argument du nombre complexe . Représenter sur la figure.
Expliquer, pour tout entier naturel , comment construire le point à partir du point .
On sait que pour tout entier naturel : avec :
En remplaçant il vient :
Donc .
Pour représenter sur la figure on considère l'angle
Pour construire le point à partir du point , il faut « tourner » de dans le sens direct sur le cercle de centre O et de rayon 5.