Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2015 en Amérique du nord
Cacher les corrigés
Partie A
Sur le graphique ci-dessous, on a tracé la courbe représentative d'une fonction définie et dérivable sur l'intervalle ainsi que les tangentes au point A d'abscisse 0, au point B d'abscisse 5 et au point D d'abscisse 10.
On sait aussi que la tangente au point A passe par le point E de coordonnées et que la tangente au point B est parallèle à l'axe des abscisses.
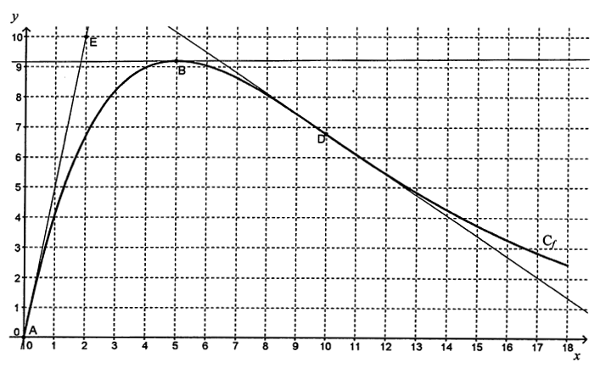
1. Donner les valeurs de et de .
La tangente au point B d'abscisse 5 est parallèle à l'axe des abscisses donc
La tangente au point passe par , donc son coefficient directeur est :
.
2. On admet que D est un point d'inflexion. Donner une interprétation graphique de ce résultat.
Au point D il y a un changement de convexité et la tangente « traverse » la courbe représentative de la fonction .
Partie B
Une entreprise s'apprête à lancer sur le marché français un nouveau jouet destiné aux écoliers. Les ventes espérées ont été modélisées par la fonction dont la courbe représentative a été tracée ci-dessus.
En abscisses, représente le nombre de jours écoulés depuis le début de la campagne publicitaire.
En ordonnées, représente le nombre de milliers de jouets vendus le -ième jour.
Ainsi, par exemple, le 10-ème jour après le début de la campagne publicitaire, l'entreprise prévoit de vendre environ jouets.
On admet que la fonction est définie sur l'intervalle par
1. Montrer que où désigne la fonction dérivée de sur l'intervalle .
La fonction est dérivable sur et :
avec :
;
;
Du coup :
2. Etudier le signe de sur puis dresser le tableau de variations de sur .
Pour tout ; , donc le signe de sur cet intervalle est le même que celui de .
Ce binôme du premier degré s'annule pour et le coefficient facteur de est négatif donc on a le tableau :
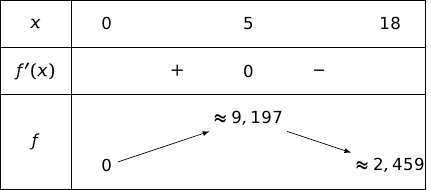
3. Déterminer le nombre de jours au bout duquel le maximum de ventes par jour est atteint. Préciser la valeur de ce maximum, arrondie à l'unité.
D'après l'étude précédente sur , la fonction admet un maximum pour .
Interprétation :
Le maximum de ventes par jour est atteint au bout de 5 jours et ce jour là environ 9197 jouets sont vendus.
Partie C
1. On admet que la fonction définie sur par
est une primitive de la fonction .
a. Calculer la valeur exacte de l'intégrale .
b. En déduire une estimation du nombre moyen de jouets vendus par jour durant la période des 10 premiers jours. On arrondira le résultat à l'unité.
Pour répondre à la question nous devons calculer la valeur moyenne de la fonction sur l'intervalle soit :
Donc sur les 10 premiers jours le nombre moyen de jouets vendus par jour est d'environ 7425.
2. Un logiciel de calcul formel nous donne les résultats suivants :
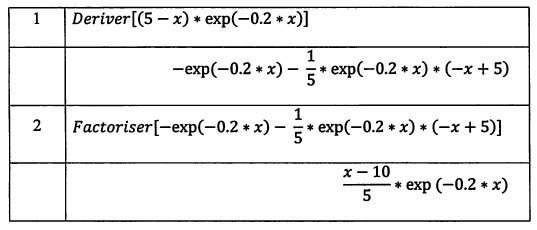
Utiliser ces résultats pour déterminer, en justifiant, l'intervalle sur lequel la fonction est convexe.
Le premier calcul nous donne l'expression de la dérivée seconde de la fonction.
Pour étudier son signe on utilise la forme factorisée donnée par le second calcul :
Pour tout ; , donc le signe est le même que celui de soit :

Ainsi , ce qui montre que la fonction est convexe sur .
