Sujet et corrigé de l'exercice 3 du bac ES de maths de juin 2015 en Asie
Cacher les corrigés
Partie A
Soit la fonction définie sur par
Un logiciel de calcul formel donne les résultats ci-dessous :
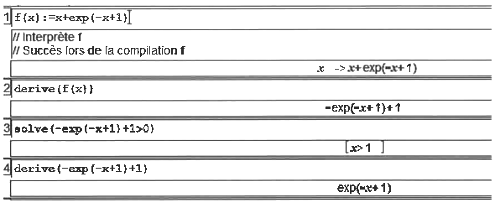
1. Etude des variations de la fonction
a. En s'appuyant sur les résultats ci-dessus, déterminer les variations de la fonction puis dresser son tableau de variation.
En exploitant les réponses du logiciel de calcul formel on a :
on suppose que de même et .
Du coup on a le tableau de variations :
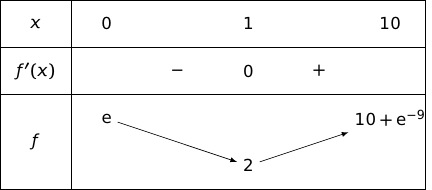
b. En déduire que la fonction admet un minimum dont on précisera la valeur.
D'après l'étude précédente la fonction admet un minimum pour et ce minimum vaut 2.
2. Etudier la convexité de la fonction sur l'intervalle .
D'après le calcul 4 du logiciel de calcul formel : .
Or pour tout ; , c'est à dire que et donc est convexe sur l'intervalle considéré.
Partie B
Une entreprise fabrique des objets. Sa capacité de production est limitée, compte tenu de l'outil de production utilisé, à mille objets par semaine.
Le coût de revient est modélisé par la fonction où est le nombre d'objets fabriqués exprimé en centaines d'objets et le coût de revient exprimé en milliers d'euros.
1. Quel nombre d'objets faut-il produire pour que le coût de revient soit minimum ?
D'après l'étude de la fonction à la partie A ; il faut vendre 100 objets.
2. Un objet fabriqué par cette entreprise est vendu 12 €. On appelle marge brute pour centaines d'objets, la différence entre le montant obtenu par la vente de ces objets et leur coût de revient.
a. Justifier que le montant obtenu par la vente de centaines d'objets est milliers d'euros.
Un objet est vendu 12 €, donc 100 objets sont vendus 1 200 € et centaines d'objets sont vendus €, soit milliers d'euros.
b. Montrer que la marge brute pour centaines d'objets, notée , en milliers d'euros, est donnée par : .
c. Montrer que la fonction est strictement croissante sur l'intervalle .
La fonction est dérivable sur et on a :
Pour tout ; et donc en ajoutant 0,2 on a encore , soit , donc est croissante sur .
3.a. Montrer que l'équation possède une unique solution sur l'intervalle .
Dressons le tableau de variations de pour voir ce qu'il se passe :
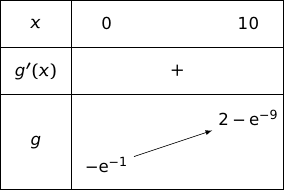
La fonction est continue et strictement croissante sur avec :
négatif
positif
Ainsi et d'après le théorème de la valeur intermédiaire il existe un unique solution de l'équation .
b. Déterminer un encadrement de d'amplitude .
En utilisant la calculette, par balayage on trouve :
4. En déduire la quantité minimale d'objets à produire afin que cette entreprise réalise une marge brute positive sur la vente de ces objets.
D'après l'étude précédente de la fonction , la marge brute est positive à partir de 1,95 centaines soit 195 objets.
