Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2015 en Asie
Cacher les corrigés
Soit la fonction définie sur par :
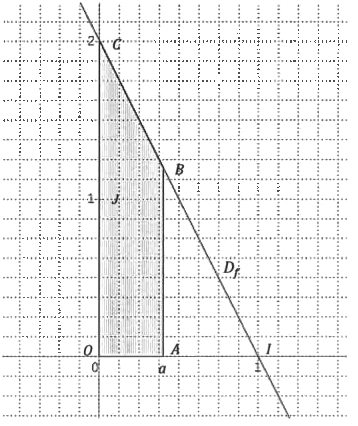
On a tracé ci-dessous la droite , représentation graphique de la fonction dans un repère orthonormé du plan.
Le point C a pour coordonnées .
est la partie du plan intérieure au triangle OIC.
Soit un nombre réel compris entre 0 et 1 ; on note A le point de coordonnées et B le point de de coordonnées .
Le but de cet exercice est de trouver la valeur de , telle que le segment [AB] partage en deux parties de même aire.
Déterminer la valeur exacte de , puis une valeur approchée au centième.
Compte tenu de la configuration ; l'aire du triangle OIC est :
u.a.
Donc la demi-aire est .
L'aire du triangle ABI est :
Du coup on cherche tel que :
Comme , cette solution ne convient pas il reste donc :
qui appartient bien à .
