Sujet et corrigé de l'exercice 3 du bac ES de maths de juin 2015 dans les centres étrangers
Cacher les corrigés
Les trois parties de cet exercice peuvent être traitées de manière indépendante.
Dans cet exercice, les résultats seront arrondis au millième.
Partie A
Une entreprise spécialisée dans la fabrication de confitures fait appel à des producteurs locaux. À la livraison, l'entreprise effectue un contrôle qualité à l'issue duquel les fruits sont sélectionnés ou non pour la préparation des confitures.
Une étude statistique a établi que :
22 % des fruits livrés sont issus de l'agriculture biologique ;
parmi les fruits issus de l'agriculture biologique, 95 % sont sélectionnés pour la préparation des confitures ;
parmi les fruits non issus de l'agriculture biologique, 90 % sont sélectionnés pour la préparation des confitures.
On prélève au hasard un fruit et on note :
B l'événement « le fruit est issu de l'agriculture biologique » ;
S l'événement « le fruit est sélectionné pour la préparation des confitures ».
Pour tout événement E, on note sa probabilité, la probabilité de l'événement E sachant que l'événement F est réalisé et l'événement contraire de E.
1. Représenter la situation par un arbre pondéré.
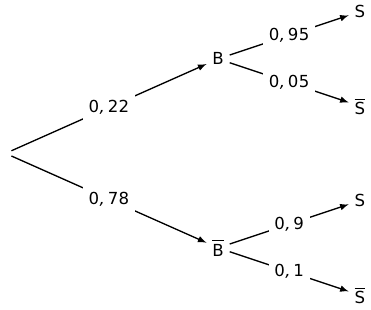
2. Déterminer la probabilité que le fruit soit sélectionné pour la préparation des confitures et qu'il soit issu de l'agriculture biologique.
Il s'agit de calculer :
3. Montrer que .
Les événements B et forment une partition de l'univers donc d'après la formule des probabilités totales :
4. Sachant que le fruit a été sélectionné pour la préparation des confitures, déterminer la probabilité qu'il ne soit pas issu de l'agriculture biologique.
Il s'agit de calculer :
Partie B
Cette entreprise conditionne la confiture en pots de 300 grammes.
On note la variable aléatoire qui, à chaque pot de confiture, associe sa masse en gramme.
On admet que suit la loi normale d'espérance et d'écart-type .
L'entreprise ne commercialise les pots de confiture que si l'écart entre la masse affichée (c'est-à-dire 300 g) et la masse réelle ne dépasse pas 4 grammes.
1. On prélève un pot au hasard. Déterminer la probabilité que le pot soit commercialisé.
Il s'agit de calculer :
(Résultat connu).
2. Déterminer le réel a tel que p(X < a) = 0,01.
En utilisant la fonction « Inverse Normale » de la calculette on obtient :
Sur CASIO ; régler « tail » à « left ».
Partie C
Dans cette question, toute trace de recherche, même incomplète, sera prise en compte dans l'évaluation.
Le directeur commercial affirme que 90 % des consommateurs sont satisfaits de la qualité des produits commercialisés par son entreprise.
On réalise une étude de satisfaction sur un échantillon de 130 personnes.
Parmi les personnes interrogées, 15 déclarent ne pas être satisfaites des produits.
Déterminer, en justifiant, si l'on doit remettre en question l'affirmation du directeur commercial.
On teste l'hypothèse : « 90 % des consommateurs sont satisfaits », en réalisant un échantillon de 130 personnes.
Pour cela on peut utiliser l'intervalle de fluctuation asymptotique à 95 % :
où et .
Les conditions d'utilisation habituelles de cet intervalle sont bien réalisées :
; donc
; donc
; donc
Et l'intervalle considéré est :
soit
Sur l'échantillon on observe personnes satisfaites, soit une proportion de .
Comme ; au vu de cette étude on ne remet pas en question l'affirmation du directeur commercial.
