Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2015 dans les centres étrangers
Cacher les corrigés
Les parties A et B ne sont pas indépendantes
Partie A
On considère la fonction définie sur par
1. Montrer que où désigne la fonction dérivée de la fonction .
La fonction est dérivable sur et pour tout :
2. Dresser le tableau de variations de la fonction sur l'intervalle .
On donnera les valeurs exactes des éléments du tableau.
On remarque déjà que sur l'intervalle considéré, , donc le signe de est le même que celui de .
Il s'agit donc d'étudier le signe d'un trinôme du second degré.
Pour cela on calcule le discriminant :
Comme , le trinôme a deux racines qui sont :
et
Du coup on a le tableau de variations :
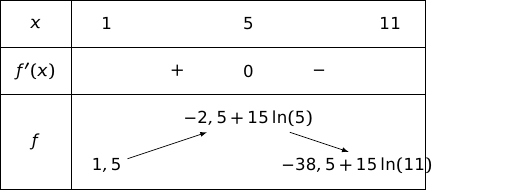
3.a. Montrer que l'équation admet une unique solution sur l'intervalle .
Sur , le minimum de est ; donc l'équation ne peut pas avoir de solution sur cet intervalle.
Sur , la fonction est continue et strictement décroissante avec :
Du coup et d'après le théorème de la valeur intermédiaire l'équation admet une unique solution dans .
b. Donner une valeur approchée de à 0,01 près.
En utilisant la calculette on obtient l'encadrement :
Donc on prend 10,66 comme valeur approchée de à 0,01 près.
c. Déterminer le signe de suivant les valeurs de dans l'intervalle .
En exploitant ce qui précède on a le tableau de signes :

4.a. On considère la fonction définie sur par
Montrer que est une primitive de la fonction
La fonction est dérivable sur et on a :
avec :
;
;
Cela montre que est bien une primitive de .
b. Calculer .
On donnera le résultat exact puis sa valeur arrondie au centième.
c. En déduire la valeur moyenne de la fonction sur l'intervalle .
(On donnera la valeur arrondie au centième.)
La valeur moyenne est :
Partie B
Une société fabrique et vend des chaises de jardin. La capacité de production mensuelle est comprise entre 100 et 1 100 chaises.
Le bénéfice mensuel réalisé par la société est modélisé par la fonction définie dans la partie A, où représente le nombre de centaines de chaises de jardin produites et vendues et représente le bénéfice mensuel, exprimé en milliers d'euros.
On précise qu'un bénéfice peut être positif ou négatif, ce qui correspond, dans ce deuxième cas, à une perte.
1. Quelles quantités de chaises la société doit-elle produire et vendre pour obtenir un bénéfice mensuel positif ?
En exploitant le tableau de signes déterminé à la question A.3.c., on peut dire que la société doit produire et vendre entre 100 et environ 1066 chaises pour réaliser un bénéfice positif.
2. Déterminer le nombre de chaises que la société doit produire et vendre pour obtenir un bénéfice mensuel maximal.
Cette fois on exploite le tableau de variations de la question A.2.
La société doit produire et vendre 500 chaises pour obtenir un bénéfice mensuel maximal.
