Sujet et corrigé de l'exercice 3 du bac ES de maths de mai 2015 au Liban
Cacher les corrigés
Les trois parties peuvent être traitées indépendamment.
Les résultats seront arrondis, si nécessaire, à .
Une entreprise fabrique en grande quantité des médailles circulaires.
La totalité de la production est réalisée par deux machines et .
La machine fournit 40 % de la production totale et le reste.
La machine produit 2 % de médailles défectueuses et la machine produit 3 % de médailles défectueuses.
Partie A
On prélève au hasard une médaille produite par l'entreprise et on considère les événements suivants :
A : « la médaille provient de la machine » ;
B : « la médaille provient de la machine » ;
D : « la médaille est défectueuse » ;
est l’événement contraire de l’événement D.
1.a. Traduire cette situation par un arbre pondéré.
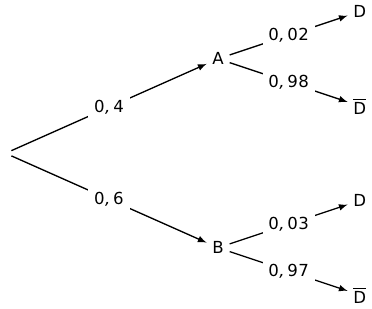
b. Montrer que la probabilité qu'une médaille soit défectueuse est égale à 0,026.
Les événements A et B forment une partition de l'univers donc d'après la formule des probabilités totales :
c. Calculer la probabilité qu'une médaille soit produite par la machine sachant qu'elle est défectueuse.
2. Les médailles produites sont livrées par lots de .
On prélève au hasard un lot de 20 médailles dans la production.
On suppose que la production est assez importante pour que l'on puisse assimiler ce prélèvement à un tirage aléatoire avec remise. Les tirages sont supposés indépendants.
On note la variable aléatoire prenant pour valeur le nombre de médailles défectueuses contenues dans ce lot.
a. Préciser la loi que suit et donner ses paramètres.
Il s'agit de la répétition de 20 expériences de Bernoulli identiques et indépendantes dont la probabilité du succès (la médaille est défectueuse) est 0,026.
La variable aléatoire qui compte le nombre de médailles défectueuses suit la loi binomiale de paramètres et .
b. Calculer la probabilité qu'il y ait au plus une médaille défectueuse dans ce lot.
Partie B
Le diamètre exprimé en millimètre, d'une médaille fabriquée par cette entreprise est conforme lorsqu'il appartient à l'intervalle .
On note la variable aléatoire qui, à chaque médaille prélevée au hasard dans la production, associe son diamètre en millimètre. On suppose que la variable aléatoire suit une loi normale de moyenne et d'écart-type 0,25.
La courbe ci-dessous est la représentation graphique de la densité de probabilité de .
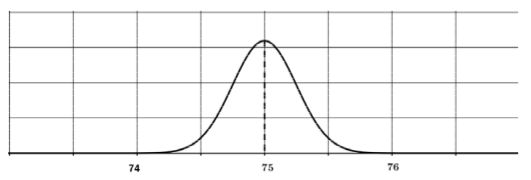
1. Indiquer par lecture graphique la valeur de .
La courbe représentative de la fonction de densité est symétrique par rapport à la droite d'équation .
Par lecture graphique : .
2. Déterminer à l'aide de la calculatrice la probabilité .
3. En utilisant un résultat du cours, déterminer la valeur de pour que
La probabilité de l'intervalle considéré centré sur vaut 0,95 ce qui correspond à l'intervalle « à 2 sigmas ».
Donc
Partie C
Dans le cadre d'un fonctionnement correct de la machine , on admet que la proportion des médailles ayant une épaisseur non conforme dans la production est de 3 %.
Pour contrôler le bon fonctionnement de la machine , on a prélevé au hasard un échantillon de 180 médailles et on a constaté que 11 médailles ont une épaisseur non conforme.
1. Calculer, dans l'échantillon prélevé, la fréquence des médailles dont l'épaisseur n'est pas conforme.
La fréquences de médailles non conformes dans l'échantillon est .
2. Déterminer, en justifiant, si le résultat de la question précédente rend pertinente la prise de décision d'arrêter la production pour procéder au réglage de la machine .
On teste l'hypothèse selon laquelle la machine donne une proportion de médailles non conformes de 3 %.
Pour cela on peut utiliser un intervalle de fluctuation asymptotique à 95 % :
avec et .
On vérifie déjà que les conditions usuelles d'utilisation de cet intervalle sont vérifiées :
; donc
; donc
; donc
L'intervalle de fluctuation est :
soit
Comme , on rejette l'hypothèse selon laquelle la machine fonctionne correctement ; il est donc pertinent de prendre la décision d'arrêter la production pour procéder au réglage de la machine.
