Sujet et corrigé de l'exercice 2 du bac es de maths de mai 2015 au Liban
Cacher les corrigés
Une entreprise artisanale produit des parasols. Elle en fabrique entre 1 et 18 par jour. Le coût de fabrication unitaire est modélisé par une fonction définie et dérivable sur l'intervalle .
On note le nombre de parasols produits par jour et le coût de fabrication unitaire exprimé en euros.
Dans le repère orthogonal ci-dessous, on a tracé la courbe représentative de la fonction et la tangente au point A(5 ; 55). Le point B(10 ; 25) appartient à la tangente .
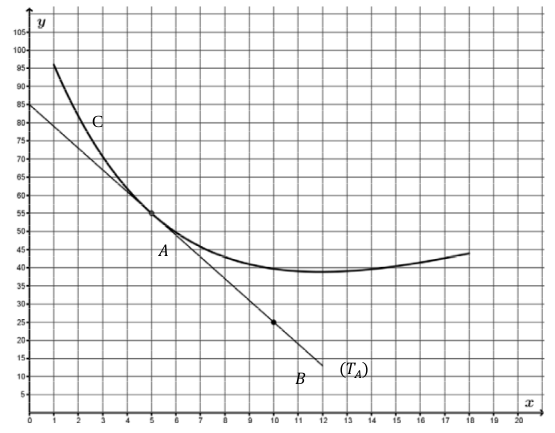
On admet que :
pour tout appartenant à l'intervalle
1.a. Déterminer graphiquement la valeur de en expliquant la démarche utilisée.
On détermine par lecture graphique le coefficient directeur de la droite en exploitant les points A et B :
b. Déterminer l'expression de pour tout appartenant à l'intervalle .
La fonction est dérivable sur avec :
où et
donc :
c. Expliquer comment retrouver la réponse obtenue dans la question 1. a.
Il suffit de calculer l'image de 5 par ce qui donne :
2.a. Montrer que est équivalente à .
b. En déduire le signe de et le tableau de variations de sur . Les valeurs seront arrondies au centime d'euro dans le tableau de variations.
Dans la question précédente on a résolu l'inéquation : .
On aurait de même :
Du coup on a le tableau de variations :
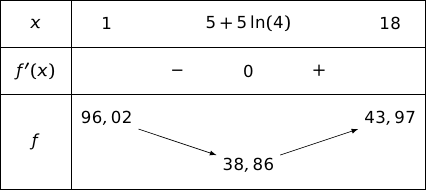
3. Déterminer, par le calcul, le nombre de parasols que doit produire l'entreprise pour que le coût de fabrication unitaire soit minimal.
D'après la question précédente, le coût de fabrication unitaire est minimal pour une production de parasols.
4.a. Montrer que la fonction définie par est une primitive de sur l'intervalle .
La fonction est dérivable sur l'intervalle considéré et pour tout :
avec et .
Ce qui prouve que est bien une primitive de .
b. Déterminer la valeur exacte de l'intégrale .
En utilisant la primitive de la question précédente :
c. Interpréter dans le contexte de l'exercice la valeur de .
représente la valeur moyenne de la fonction sur l'intervalle .
C'est le coût moyen de fabrication d'un parasol lorsque la production est comprise entre 5 et 15 parasols.
