Sujet et corrigé de l'exercice 1 du bac ES de maths de juin 2015 en Polynésie
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Aucune justification n'est demandée.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point.
1. Soit la fonction définie pour tout nombre réel par
Si désigne la fonction dérivée de , on a :
a.
b.
c.
d.
La bonne réponse est la réponse c.
2. La courbe représentative d'une fonction définie sur l'intervalle est donnée ci-dessous.
La tangente à la courbe au point d'abscisse traverse la courbe en ce point.
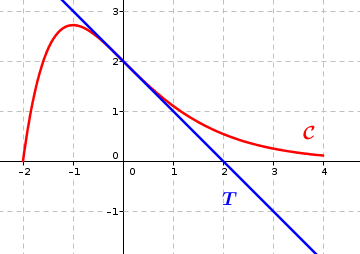
La fonction est convexe sur l'intervalle :
a.
b.
c.
d.
Par simple observation graphique on détermine que est convexe sur .
La bonne réponse est la réponse d.
3. On donne l'algorithme ci-dessous.
| Variables : | est un nombre entier naturel |
| Traitement : | Affecter à la valeur |
| Tant que | |
| Affecter à la valeur | |
| Fin Tant que | |
| Sortie : | Afficher |
La valeur affichée en sortie de cet algorithme est :
a. 7,1
b. 7,6
c. 8
d. 17
Cet algorithme retourne la première valeur de entier pour laquelle .
En utilisant la calculette on a :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
Donc l'algorithme affiche 8.
La bonne réponse est la réponse c.
4. Une variable aléatoire suit la loi uniforme sur l'intervalle [0 ; 5] dont la fonction de densité est représentée ci-dessous.
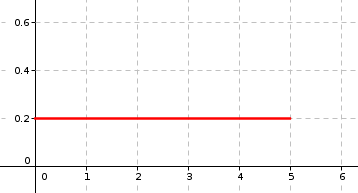
On a alors :
a.
b.
c.
d.
On sait que l'espérance de la loi uniforme sur est ; donc ici ça donne .
La bonne réponse est la réponse c.
