Sujet et corrigé de l'exercice 2 du bac ES de maths de juin 2015 en Polynésie
Cacher les corrigés
Les parties A et B sont indépendantes.
Sur une exploitation agricole, une maladie rend la conservation de fruits difficile.
Un organisme de recherche en agronomie teste un traitement sur un champ : sur une partie du champ, les fruits sont traités, sur l'autre, non.
On considère que le nombre de fruits récoltés est extrêmement grand et que la maladie touche les fruits de manière aléatoire.
Partie A : Etude de l'efficacité du traitement
On prélève au hasard 100 fruits sur la partie du champ traité et 100 fruits sur l'autre partie du champ. On constate que :
sur l'échantillon des 100 fruits traités, 18 sont abîmés ;
sur l'échantillon des 100 fruits non traités, 32 sont abîmés.
1. Déterminer un intervalle de confiance de la proportion de fruits abîmés par la maladie au niveau de confiance de 95 % :
a. pour la partie du champ traitée;
b. pour la partie du champ non traitée.
a. Pour la partie du champs traitée la fréquence observée de fruits abîmés dans l'échantillon est .
On vérifie que les conditions d'utilisation habituelles de l'intervalle de confiance sont vérifiées :
; donc ;
; donc ;
; donc .
Un intervalle de confiance au niveau de 95 % est :
soit
b. Pour la partie du champs non traitée la fréquence observée de fruits abîmés dans l'échantillon est .
Vérification des conditions :
; donc ;
; donc ;
; donc .
Un intervalle de confiance au niveau de 95 % est :
soit
2. Au vu des intervalles obtenus à la question 1, peut-on considérer que le traitement est efficace ?
Les fourchettes données par les intervalles de confiance considérés se chevauchent donc au niveau de confiance de 95 % on ne peut pas considérer que le traitement est efficace.
Partie B : Qualité de la production
Une étude plus poussée permet d'estimer la proportion de fruits abimés à 0,12 dans la partie du champ traitée et à 0,30 dans la partie non traitée.
On sait de plus qu'un quart du champ a été traité.
Une fois récoltés, les fruits sont mélangés sans distinguer la partie du champ d'où ils proviennent.
On prélève au hasard un fruit récolté dans le champ et on note :
T l'événement « Le fruit prélevé provient de la partie traitée » ;
A l'événement « Le fruit prélevé est abimé »
On arrondira les résultats au millième.
1. Construire un arbre pondéré traduisant la situation.
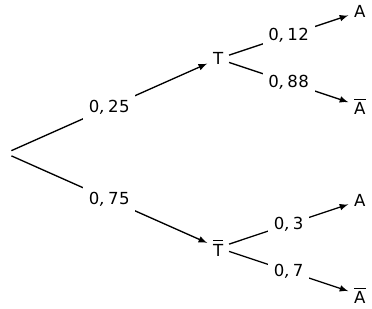
2.a. Calculer la probabilité que le fruit prélevé soit traité et abimé.
b. Montrer que .
Les événements T et forment une partition de l'univers.
D'après la formule des probabilités totales :
3. Un fruit prélevé au hasard dans la récolte est abîmé.
Peut-on affirmer qu'il y a une chance sur quatre pour qu'il provienne de la partie du champ traitée ?
On calcule :
Donc il n'y a pas une chance sur quatre pour que le fruit provienne de la partie du champ traitée.
4. Dans le but d'effectuer un contrôle, cinq fruits sont prélevés au hasard dans le champ.
Calculer la probabilité qu'au plus un fruit soit abîmé.
Le nombre de fruits est suffisamment grand pour que l'on puisse assimiler le prélèvement des cinq fruits à un tirage avec remise.
Du coup on a une répétition de 5 expériences de Bernoulli identiques et indépendantes dont la probabilité du succès (le fruit est abîmé) est 0,255.
La variable aléatoire qui compte le nombre de fruits abîmés suit une loi Binomiale de paramètres et .
On calcule donc :
