Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2015 en Polynésie
Cacher les corrigés
Une compagnie aérienne propose à partir du premier janvier de l'année 2000 une nouvelle formule d'achat de billets, la formule « Avantage » qui s'ajoute à la formule « Privilège » déjà existante.
Une étude a permis de modéliser l'évolution du nombre de passagers transportés depuis l'année 2000 et la compagnie admet que ce modèle est valable sur la période allant de l'année 2000 à l'année 2016.
Le nombre de passagers choisissant la formule « Privilège » est modélisé par la fonction définie sur l'intervalle et le nombre de passagers choisissant la formule « Avantage » est modélisé par la fonction définie sur l'intervalle .
Le graphique donné ci-dessous représente les courbes représentatives et de ces deux fonctions.
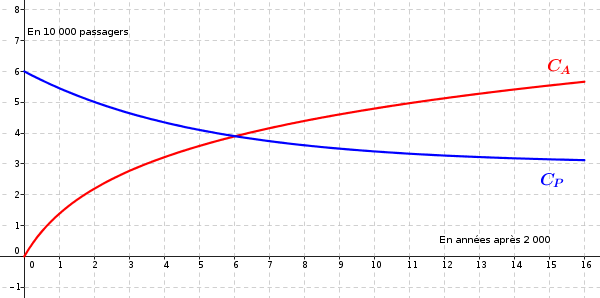
Lorsque représente le temps en année à partir de l'année 2000, représente le nombre de passagers, exprimé en dizaine de milliers, choisissant la formule « Privilège » et représente le nombre de passagers, exprimé en dizaine de milliers, choisissant la formule « Avantage ».
Partie A
Dans cette partie, les estimations seront obtenues par lecture graphique.
1. Donner une estimation du nombre de passagers qui, au cours de l'année 2002, avaient choisi la formule « Privilège ».
50 000 passagers.
2. Donner une estimation de l'écart auquel la compagnie peut s'attendre en 2015 entre le nombre de passagers ayant choisi la formule « Avantage » et ceux ayant choisi la formule « Privilège ».
Un écart de l'ordre de 25 000 passagers.
3. Comment peut-on interpréter les coordonnées du point d'intersection des deux courbes au regard de la situation proposée ?
Fin 2005/début 2006, le nombre de passagers qui voyagent en formule « Privilège » et en formule « Avantage » est le même et de l'ordre de 40 000.
4. Justifier que la compagnie aérienne peut, selon ce modèle, estimer que le nombre total de passagers ayant choisi la formule « Privilège » durant la période entre 2007 et 2015 sera compris entre 240 000 et 320 000.
Il s'agit d'évaluer l'aire du domaine délimité par la courbe , l'axe des abscisses et les droites d'équations et .
On peut encadrer cette aire par les aires de deux rectangles de « largeur » 8.
Le premier a une « hauteur » de 3 ; donc son aire est 24 u.a.
Le second a une « hauteur » de 4 ; donc son aire est 32 u.a.
Du coup le nombre total de passagers ayant choisi la formule « Privilège » durant la période considérée est compris entre 240 000 et 320 000.
Partie B
On admet que la fonction est définie sur l'intervalle par
et que la fonction est définie sur l'intervalle par
On s'intéresse à la différence en fonction du temps qu'il y a entre le nombre de passagers ayant choisi la formule « Avantage » et ceux ayant choisi la formule « Privilège ». Pour cela, on considère la fonction définie sur l'intervalle par .
1. On note la fonction dérivée de sur l'intervalle .
a. On admet que .
Justifier que est strictement positive sur l'intervalle .
Pour tout :
; donc
; ; donc
La somme sera encore strictement positive donc .
b. Dresser le tableau de variation de la fonction sur l'intervalle .
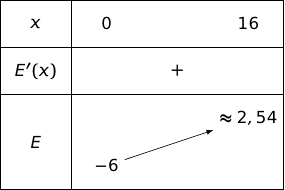
2.a. Montrer que l'équation admet une unique solution, notée , sur l'intervalle . Donner la valeur de en arrondissant au dixième.
La fonction est continue et strictement croissante sur avec :
or ; donc d'après le théorème de la valeur intermédiaire, l'équation admet une unique solution dans .
Avec la calculette, par balayage, on a l'encadrement :
Donc une valeur approchée au dixième est .
b. Dresser le tableau de signes de la fonction sur l'intervalle .
Interpréter les résultats obtenus au regard des deux formules proposées par la compagnie aérienne.

Pour cette interprétation on considère que .
Pour ; , soit .
Donc de 2000 à fin 2005, la formule « Privilège » est la plus utilisée.
Pour ; , soit
Donc fin 2005/début 2006 les deux formules sont choisies par à peu près le même nombre de passagers.
Pour ; , soit .
Donc de début 2006 jusqu'en 2016 c'est la formule « Avantage » qui est la plus utilisée.
