Sujet et corrigé de l'exercice 2 du bac ES de maths d'avril 2016 à Pondichéry
Cacher les corrigés
La partie A peut être traitée indépendamment des parties B et C.
L'entreprise BBE (Bio Bois Energie) fabrique et vend des granulés de bois pour alimenter des chaudières et des poêles chez des particuliers ou dans des collectivités.
L'entreprise produit entre 1 et 15 tonnes de granulés par jour.
Les coûts de fabrication quotidiens sont modélisés par la fonction
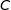définie sur l'intervalle 
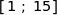par :
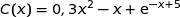
où
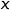désigne la quantité de granulés en tonnes et 
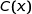le coût de fabrication quotidien correspondant en centaines d'euros.
Dans l'entreprise BBE le prix de vente d'une tonne de granulés de bois est de 300 euros.
La recette quotidienne de l'entreprise est donc donnée par la fonction
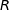définie sur l'intervalle 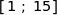par :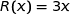
où
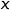désigne la quantité de granulés en tonnes et 
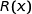la recette quotidienne correspondante en centaines d'euros.
On définit par
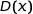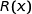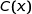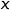le résultat net quotidien de l'entreprise en centaines d'euros, c'est à dire la différence entre la recette et le coût , où désigne la quantité de granulés en tonnes.
Partie A : Etude graphique
Sur le graphique ci-dessous, on donne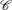 
et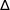 
les représentations graphiques respectives des fonctions 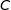et 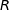dans un repère d'origine O.
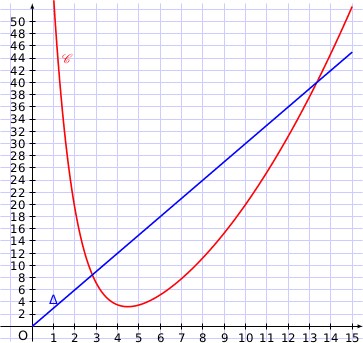
Dans cette partie A, répondre aux questions suivantes à l'aide du graphique, et avec la précision permise par celui-ci. Aucune justification n'est demandée.
1. Déterminer la quantité de granulés en tonnes pour laquelle le coût quotidien de l'entreprise est minimal.
Le coût est minimal pour environ 4,5 tonnes de granulés.
2.
a) Déterminer les valeurs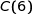 
et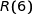 
puis en déduire une estimation du résultat net quotidien en euros dégagé par l'entreprise pour 6 tonnes de granulés fabriqués et vendus.
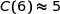et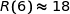 
.
Estimation du résultat net pour 6 tonnes de granulés :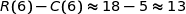 
, soit 1 300 euros.
b) Déterminer les quantités possibles de granulés en tonnes que l'entreprise doit produire et vendre quotidiennement pour dégager un resultat net positif, c'est à dire un bénéfice.
On regarde les parties du graphique où la droite 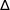est située au dessus de la courbe .
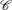Pour dégager un résultat net positif l'entreprise doit produire entre environ 2,8 et 13,3 tonnes de granulés.
Partie B : Etude d'une fonction
On considère la fonction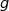 
définie sur l'intervalle 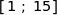par :
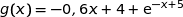
On admet que la fonction 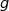est dérivable sur l'intervalle 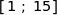et on note 
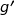sa fonction dérivée.
1.
a) Calculer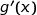 
pour tout réel 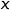de l'intervalle .
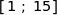Pour tout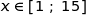 
, 
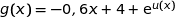avec :
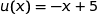et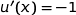 
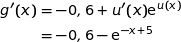
b) En déduire que la fonction 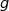est croissante sur l'intervalle .
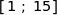Pour tout réel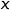 
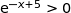et donc 
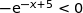, du coup 
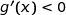pour tout .
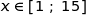Cela entraîne que 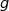est décroissante sur l'intervalle considéré.
2.
a) Dresser le tableau de variation de la fonction 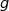sur l'intervalle 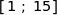, en précisant les valeurs de 
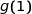et de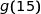 
arrondies à l'unité.
Tableau de variation :
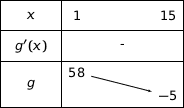
b) Le tableau de variation permet d'affirmer que l'équation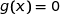 
admet une unique solution 
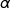sur l'intervalle .
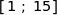Donner une valeur approchée de 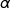à 0,1 près.
En utilisant la calculette on trouve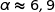 
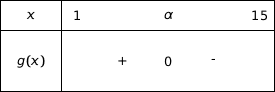
c) Déduire des questions précédentes le tableau de signes de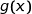 
sur l'intervalle .
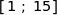En exploitant ce qui précède on a facilement le tableau de signes de :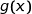
Partie C : Application économique
1. Démontrer que pour tout réel 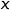de l'intervalle 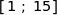, on a :
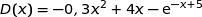
Pour tout :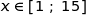
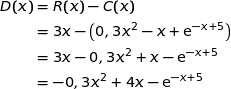
2. On admet que la fonction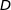 
est dérivable sur l'intervalle 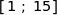et on note 
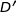sa fonction dérivée.
Démontrer que pour tout réel 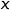de l'intervalle 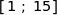, on a 
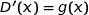, où 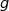est la fonction étudiée dans la partie B.
Pour tout 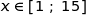, on peut écrire :
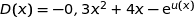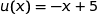où et .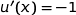
Du coup on a :
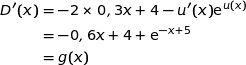
3. En déduire les variations de la fonction 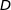sur l'intervalle .
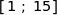En utilisant le signe de 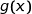obtenu à la question 2.c de la partie B, on dresse le tableau de variation de :
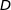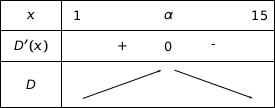
4.
a) Pour quelle quantité de granulés l'entreprise va-t-elle rendre son bénéfice maximal ?
On donnera une valeur approchée du résultat à 0,1 tonne près.
D'après l'étude précédente le bénéfice maximal est obtenu pour la production de 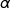tonnes de granulés soit environ 6,9 tonnes.
b) Calculer alors le bénéfice maximal à l'euro près.
Le montant du bénéfice maximal en centaines d'euros est :
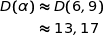
Donc à l'euro près, le bénéfice maximal est 1 317 euros.
