Sujet et corrigé de l'exercice 3 du bac ES de maths d'avril 2016 à Pondichéry
Cacher les corrigés
Les parties A et B peuvent être traitées de manière indépendante.
Partie A
On dispose des renseignements suivants à propos du baccalauréat 2015 :
49 % des inscrits ont passé un baccalauréat général, 20 % un baccalauréat technologique et les autres un baccalauréat professionnel;
91,5 % des candidats au baccalauréat général ont été reçus ainsi que 90,6 % des candidats aux baccalauréat technologique.
Source : DEPP (juillet 2015)
On choisit au hasard un candidat au baccalauréat de la session 2015 et on considère les événements suivants :
G : « Le candidat s'est présenté au baccalauréat général »;
T : « Le candidat s'est présenté au baccalauréat technologique »;
S : « Le candidat s'est présenté au baccalauréat professionnel »;
R : « Le candidat a été reçu ».
Pour tout événement A, on note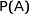 
sa probabilité et 
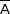son événement contraire.
De plus, si B est un autre événement, on note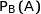 
la probabilité de A sachant B.
1. Préciser les probabilités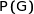 
, 
, 
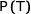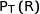et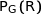 
Par simple lecture des données de l'énoncé on a :
;
;
;
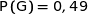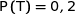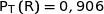2. Traduire la situation par un arbre pondéré. On indiquera les probabilités trouvées à la question précédente. Cet arbre pourra être complété par la suite.
Arbre pondéré :
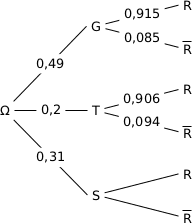
3. Vérifier que la probabilité que le candidat choisi se soit présenté au baccalauréat technologique et l'ait obtenu est égale à 0,1812.
Il s'agit de calculer :
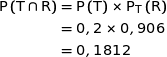
4. Le ministère de l'Education Nationale a annoncé un taux global de réussite pour cette session de 87,8 % pour l'ensemble des candidats présentant l'un des baccalauréats.
a) Vérifier que la probabilité que le candidat choisi se soit présenté au baccalauréat professionnel et l'ait obtenu est égale à 0,24845.
Les événements G, T et S forment une partition de l'univers et d'après la formule des probabilités totales on a :
Comme nous savons par ailleurs que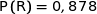 
, il vient :
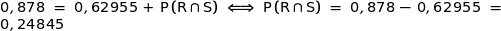
b) Sachant que le candidat s'est présenté au baccalauréat professionnel, déterminer la probabilité qu'il ait été reçu. On donnera une valeur approchée du résultat au millième.
En utilisant la relation vue en cours :
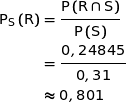
Partie B
A l'issue des épreuves du baccalauréat, une étude est faite sur les notes obtenues par les candidats en mathématiques et en français.
On admet que la note de mathématiques peut être modélisée par une variable aléatoire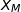 
qui suit la loi normale de moyenne 12,5 et d'écart-type 3,5.
De même la note de français peut être modélisée par une variable aléatoire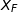 
qui suit la loi normale de moyenne 13,2 et d'écart-type 2,1.
1. Déterminer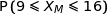 
en donnant le résultat arrondi au centième.
En utilisant la calculette on trouve :
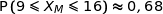
2. Sur les graphiques ci-dessous, on a représenté en pointillé la fonction densité associée à la variable aléatoire .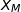
La fonction densité associée à 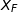est représentée sur un seul de ces graphiques.
Quel est ce graphique ? Expliquer le choix.
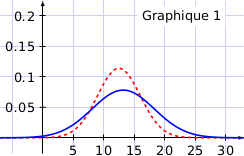
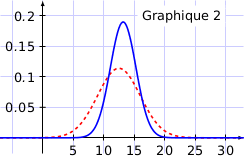
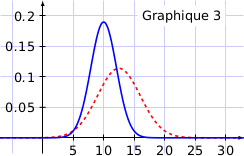
La moyenne de la loi normale considérée vaut 13,2; donc la courbe représentative de la fonction densité doit être symétrique par rapport à la droite d'équation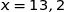 
, du coup le graphique 3 n'est pas bon.
L'écart type de 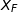est inférieur à celui de 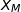, cela signifie que graphiquement, le « pic » de la courbe représentative de la fonction densité est plus « resserré », donc le bon graphique est le graphique 2.
