Corrigé de l'exercice 2 du bac ES de maths de mai 2012 en Amérique du nord
Cacher les corrigés
Un restaurateur propose trois formules à midi : Formule A : Plat du jour / Dessert / Café Formule B : Entrée / Plat du jour / Dessert / Café Formule C : Entrée / Plat du jour / Fromage / Dessert / Café Lorsqu'un client se présente au restaurant pour le repas de midi, il doit choisir une des trois formules proposées et commander ou non du vin. Le restaurateur a constaté qu'un client sur cinq choisit la formule A, tandis qu'un client sur deux choisit la formule B. On sait aussi que :- Parmi les clients qui choisissent la formule A, une personne sur quatre commande du vin.
- Parmi les clients qui choisissent la formule B, deux personnes sur cinq commandent du vin.
- Parmi les clients qui choisissent la formule C, deux personnes sur trois commandent du vin.
Si A et B désignent deux événements d'une même expérience aléatoire, alors on notera
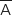l'événement contraire de A, 
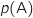la probabilité de l'événement A et 
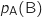la probabilité de l'événement B sachant que A est réalisé.
Les probabilités demandées seront arrondies, si c'est nécessaire, au centième.
1. Calculer 
.
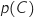L'univers associé à la situation est constitué des 3 événements élémentaires A, B et C donc :
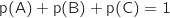soit :
.
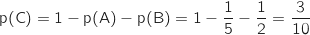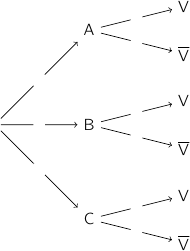
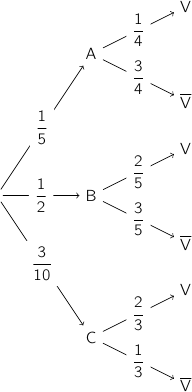
2. Reproduire et compléter l'arbre de probabilités donné ci-dessous.
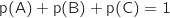soit :
.
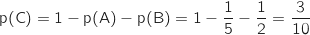3. Montrer que
.
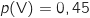Le système constitué des événements A, B et C est un système complet, donc d'après la formule des probabilités totales :
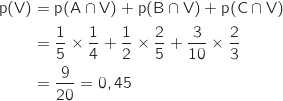
4. Le client commande du vin. Calculer la probabilité qu'il ait choisi la formule A.
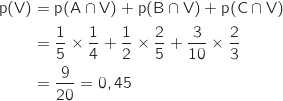
On doit calculer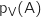 
.
On utilise la formule :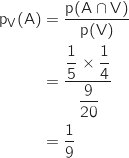 
5. La formule A coûte 8 euros, la formule B coûte 12 euros et la formule C coûte 15 euros. Le vin est en supplément et coûte 3 euros.
On note .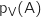
On utilise la formule :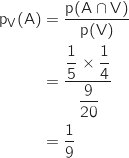
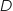la dépense en euro d'un client venant manger à midi dans ce restaurant.
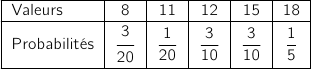
a. Déterminer la loi de probabilité de .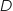
Les valeurs possibles pour 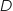sont :
:
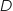On peut vérifier que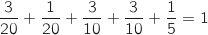 
, ce qui permet de
conjecturer qu'on n'a pas fait d'erreur.
b. Calculer la dépense moyenne par client en euro.
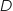sont :
- 8 : formule A sans vin :
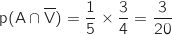
- 11 : formule A avec vin :
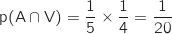
- 12 : formule B sans vin :
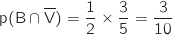
- 15 : formule B avec vin ou formule C sans vin :
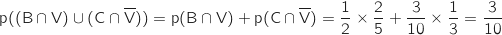
- 18 : formule C avec vin :
.
:
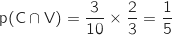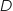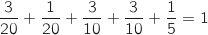, ce qui permet de
conjecturer qu'on n'a pas fait d'erreur.
Pour obtenir la dépense moyenne par client on calcule l'espérance de .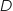
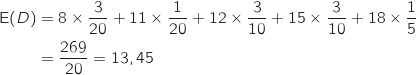Donc en moyenne un client dépense 13,45 euros.
.
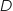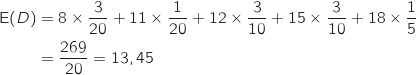Donc en moyenne un client dépense 13,45 euros.
