Corrigé de l'exercice 3 du bac ES de maths de mai 2012 en Amérique du nord
Cacher les corrigés
Partie A
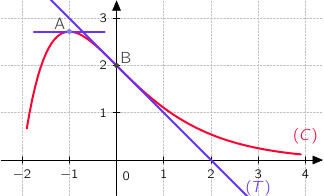
On donne ci-dessous, dans un repère orthonormé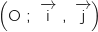 ,
la courbe représentative
,
la courbe représentative 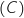 d'une fonction
d'une fonction  définie et dérivable sur l'intervalle
définie et dérivable sur l'intervalle 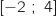 .
On nomme A le point de
.
On nomme A le point de 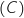 d'abscisse
d'abscisse 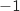 et B le point de
et B le point de 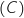 d'abscisse 0.
d'abscisse 0.
- La fonction
 est strictement croissante sur l'intervalle
est strictement croissante sur l'intervalle 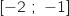 et strictement décroissante sur l'intervalle
et strictement décroissante sur l'intervalle 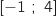 .
.
- La tangente à
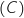 au point A est horizontale.
au point A est horizontale.
- La droite
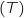 est la tangente à
est la tangente à 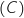 au point B et a pour équation
au point B et a pour équation 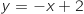 .
.
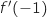 .
.
Au point A d'abscisse 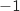 , la tangente est horizontale donc
, la tangente est horizontale donc 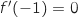 .
.
b. Déterminer le signe de 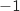 , la tangente est horizontale donc
, la tangente est horizontale donc 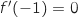 .
.
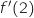 .
.
La fonction  est strictement croissante sur l'intervalle
est strictement croissante sur l'intervalle 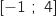 , donc pour tout
, donc pour tout 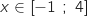 ,
,  est négatif
et en particulier
est négatif
et en particulier 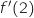 est négatif.
est négatif.
c. Interpréter graphiquement  est strictement croissante sur l'intervalle
est strictement croissante sur l'intervalle 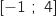 , donc pour tout
, donc pour tout 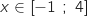 ,
,  est négatif
et en particulier
est négatif
et en particulier 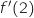 est négatif.
est négatif.
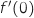 , puis donner sa valeur.
, puis donner sa valeur.
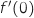 est le coefficient directeur de la droite tangente à la courbe de
est le coefficient directeur de la droite tangente à la courbe de  au point d'abscisse 0. Or on sait que l'équation
de cette tangente est
au point d'abscisse 0. Or on sait que l'équation
de cette tangente est 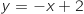 , donc
, donc 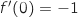 (
(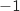 est le coefficient en facteur de
est le coefficient en facteur de  dans l'équation de la tangente, c'est le coefficient directeur de la droite en question).
dans l'équation de la tangente, c'est le coefficient directeur de la droite en question).
2. Encadrer, avec deux entiers consécutifs, l'intégrale
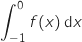 exprimée en unité d'aire.
exprimée en unité d'aire.
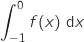 représente l'aire délimitée par la courbe de
représente l'aire délimitée par la courbe de  , les droites d'équation
, les droites d'équation 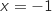 ,
, 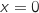 et l'axe des abscisses.
Par observation du graphique on a :
et l'axe des abscisses.
Par observation du graphique on a : 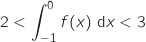 .
.
Partie B
La fonction de la Partie A a pour expression
de la Partie A a pour expression 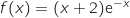 .
1. Calculer la valeur exacte de l'ordonnée du point A de la courbe
.
1. Calculer la valeur exacte de l'ordonnée du point A de la courbe 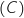 .
.
Le point A est d'abscisse 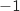 , donc l'ordonnée de
, donc l'ordonnée de 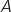 est :
est :
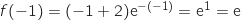 .
.
2. Justifier par le calcul le sens de variation de la fonction 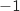 , donc l'ordonnée de
, donc l'ordonnée de 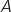 est :
est :
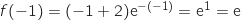 .
.
 sur l'intervalle
sur l'intervalle 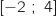 .
.
Pour déterminer le sens de variation de  on détermine la fonction dérivée.
Pour tout
on détermine la fonction dérivée.
Pour tout 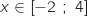 , on a :
, on a :
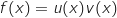 avec :
avec :
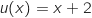 ;
; 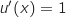 et
et 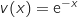 ;
; 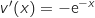 Donc
Donc 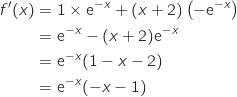 On sait que pour tout
On sait que pour tout  ,
, 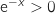 , donc le signe de
, donc le signe de  est le même
que celui de
est le même
que celui de 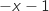 et on en déduit le tableau de variation de
et on en déduit le tableau de variation de  :
:

3. Montrer que la fonction  on détermine la fonction dérivée.
Pour tout
on détermine la fonction dérivée.
Pour tout 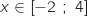 , on a :
, on a :
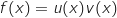 avec :
avec :
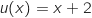 ;
; 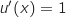 et
et 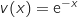 ;
; 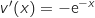 Donc
Donc 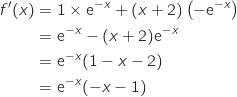 On sait que pour tout
On sait que pour tout  ,
, 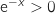 , donc le signe de
, donc le signe de  est le même
que celui de
est le même
que celui de 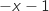 et on en déduit le tableau de variation de
et on en déduit le tableau de variation de  :
:

 définie sur l'intervalle
définie sur l'intervalle 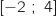 par
par 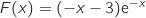 est une primitive de
est une primitive de  .
.
Pour vérifier que  est une primitive de
est une primitive de  , on dérive
, on dérive  :
:
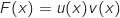 avec :
avec :
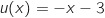 ;
; 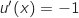 et
et 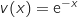 ;
; 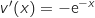 Donc
Donc 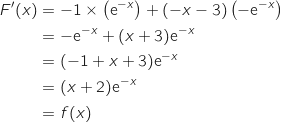 Cela prouve que
Cela prouve que  est une primitive de
est une primitive de  .
.
4.a. Calculer la valeur exacte de l'intégrale  est une primitive de
est une primitive de  , on dérive
, on dérive  :
:
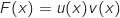 avec :
avec :
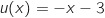 ;
; 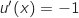 et
et 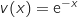 ;
; 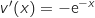 Donc
Donc 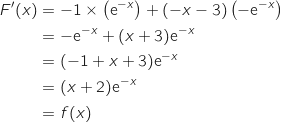 Cela prouve que
Cela prouve que  est une primitive de
est une primitive de  .
.
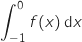 .
.
On sait d'après le cours que :
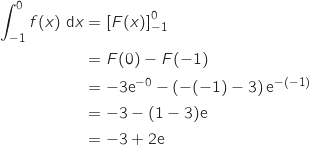
b. Vérifier la cohérence de ce résultat avec celui de la question 2) de la partie A.
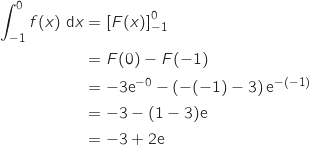
On a 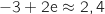 avec
avec  , donc le résultat est cohérent.
, donc le résultat est cohérent.
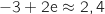 avec
avec  , donc le résultat est cohérent.
, donc le résultat est cohérent.
