Corrigé de l'exercice 4 du bac ES de maths de mai 2012 en Amérique du nord
Cacher les corrigés
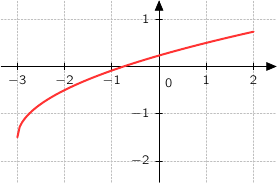
Les questions 1, 2 et 3 sont indépendantes. 1. On donne ci-dessous, dans un repère orthonormé, la courbe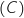 d'une fonction
d'une fonction  définie sur l'intervalle
définie sur l'intervalle 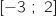 .
La courbe
.
La courbe 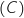 coupe l'axe des abscisses au point A d'abscisse
coupe l'axe des abscisses au point A d'abscisse 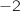 et au point B d'abscisse 1.
et au point B d'abscisse 1.
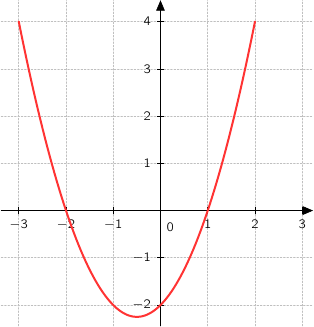
Parmi les trois courbes proposées ci-dessous, déterminer la seule qui représente une primitive de
 sur l'intervalle
sur l'intervalle 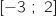 .
Courbe (a) :
.
Courbe (a) :
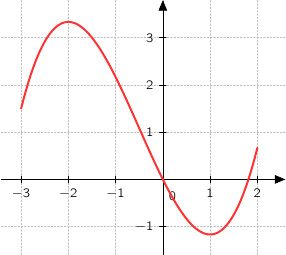
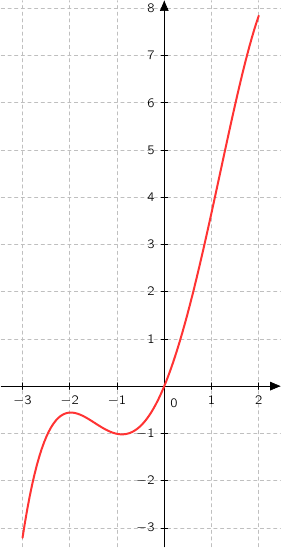
Notons  une primitive de
une primitive de  , alors
, alors 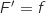 .
Le signe de
.
Le signe de  donne les variations de
donne les variations de  et par lecture graphique on a :
et par lecture graphique on a :
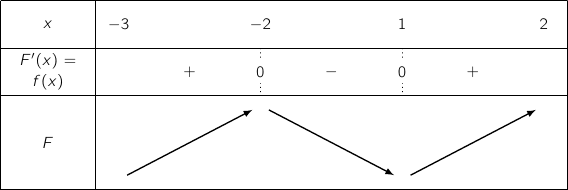
Parmi les courbes (a), (b) et (c) la seule qui correspond aux variations est la courbe (a).
Donc la bonne réponse est (a).
 une primitive de
une primitive de  , alors
, alors 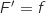 .
Le signe de
.
Le signe de  donne les variations de
donne les variations de  et par lecture graphique on a :
et par lecture graphique on a :

2. On admet que l'équation
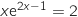 n'a qu'une solution
n'a qu'une solution  dans
dans  .
Déterminer une valeur approchée de
.
Déterminer une valeur approchée de  à
à 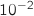 près.
près.
L'équation 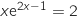 est équivalente à
est équivalente à 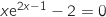 .
En utilisant la calculette on trace la courbe représentative de la fonction
.
En utilisant la calculette on trace la courbe représentative de la fonction 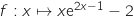 :
:
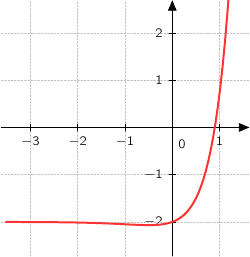
On remarque que la courbe coupe l'axe des abscisses pour une valeur  tellle que
tellle que 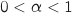 .
Avec la fonction table de la calculette on affiche les valeurs de
.
Avec la fonction table de la calculette on affiche les valeurs de 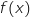 dans la plage
dans la plage  avec un pas de
avec un pas de 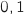 ce qui permet d'obtenir
un premier encadrement de
ce qui permet d'obtenir
un premier encadrement de  :
: 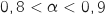 .
En poursuivant avec un pas de
.
En poursuivant avec un pas de 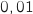 sur la plage
sur la plage 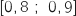 on obtient :
on obtient : 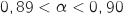 .
Pour finir avec un pas de
.
Pour finir avec un pas de 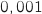 sur la plage
sur la plage 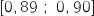 on obtient :
on obtient : 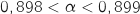 .
Donc
.
Donc 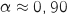 .
.
3. Dans cette question, toute trace de recherche même incomplète, sera prise en compte dans l'évaluation.
Une entreprise produit des tentes. Le coût marginal, en milliers d'euros, pour la production de 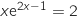 est équivalente à
est équivalente à 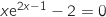 .
En utilisant la calculette on trace la courbe représentative de la fonction
.
En utilisant la calculette on trace la courbe représentative de la fonction 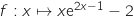 :
:

 tellle que
tellle que 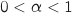 .
Avec la fonction table de la calculette on affiche les valeurs de
.
Avec la fonction table de la calculette on affiche les valeurs de 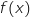 dans la plage
dans la plage  avec un pas de
avec un pas de 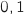 ce qui permet d'obtenir
un premier encadrement de
ce qui permet d'obtenir
un premier encadrement de  :
: 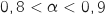 .
En poursuivant avec un pas de
.
En poursuivant avec un pas de 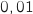 sur la plage
sur la plage 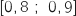 on obtient :
on obtient : 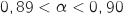 .
Pour finir avec un pas de
.
Pour finir avec un pas de 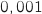 sur la plage
sur la plage 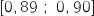 on obtient :
on obtient : 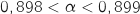 .
Donc
.
Donc 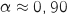 .
.
 centaines de tentes, avec
centaines de tentes, avec 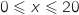 est donné par la fonction
est donné par la fonction  définie sur l'intervalle
définie sur l'intervalle 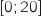 par
par 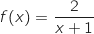 .
On note
.
On note 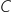 la fonction qui représente le coût total exprimé en milliers d'euros pour une production de
la fonction qui représente le coût total exprimé en milliers d'euros pour une production de  centaines de tentes, avec
centaines de tentes, avec 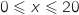 .
On assimile le coût marginal à la dérivée de la fonction coût total, c'est à dire à la dérivée de la fonction
.
On assimile le coût marginal à la dérivée de la fonction coût total, c'est à dire à la dérivée de la fonction 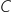 .
Sachant que les coûts fixes sont de 5 000 euros, déterminer le coût total en milliers d'euros, pour une production de
.
Sachant que les coûts fixes sont de 5 000 euros, déterminer le coût total en milliers d'euros, pour une production de  centaines de tentes, avec
centaines de tentes, avec 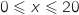 .
.
D'après l'énoncé on a 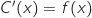 , donc
, donc 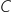 est une primitive de
est une primitive de  . De plus les coûts fixes sont de 5 000 euros, ce qui correspond au coût total
da la production de 0 tentes soit
. De plus les coûts fixes sont de 5 000 euros, ce qui correspond au coût total
da la production de 0 tentes soit 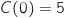 (car on travaille en milliers d'euros).
Finalement on cherche la primitive
(car on travaille en milliers d'euros).
Finalement on cherche la primitive 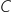 de la fonction
de la fonction  telle que
telle que 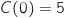 .
Les primitives de la fonction
.
Les primitives de la fonction  sont de la forme :
sont de la forme :
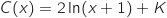
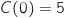 donne :
donne : 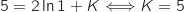 .
Donc
.
Donc 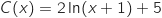 .
.
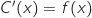 , donc
, donc 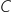 est une primitive de
est une primitive de  . De plus les coûts fixes sont de 5 000 euros, ce qui correspond au coût total
da la production de 0 tentes soit
. De plus les coûts fixes sont de 5 000 euros, ce qui correspond au coût total
da la production de 0 tentes soit 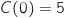 (car on travaille en milliers d'euros).
Finalement on cherche la primitive
(car on travaille en milliers d'euros).
Finalement on cherche la primitive 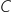 de la fonction
de la fonction  telle que
telle que 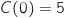 .
Les primitives de la fonction
.
Les primitives de la fonction  sont de la forme :
sont de la forme :
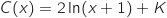
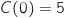 donne :
donne : 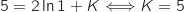 .
Donc
.
Donc 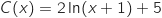 .
.
