Sujet et corrigé de l'exercice 1 du bac ES de maths de mai 2014 en Amérique du nord
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions posées, une seule des quatre réponses est exacte.
Indiquer sur la copie le numéro de la question et recopier la réponse choisie.
Aucune justification n'est demandée.
La courbe ci-dessous est la représentation graphique, dans un repère orthonormé, d'une fonction définie et dérivable sur l'intervalle .
On note la fonction dérivée de .
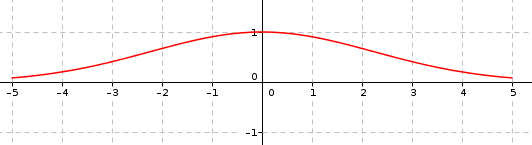
1. Sur l'intervalle :
| a) est une fonction densité de probabilité | b) est positive |
| c) n'est pas continue | d) l'équation admet 2 solutions. |
Très facilement on voit que la bonne réponse est la réponse b.
Les autres réponses sont fausses :
a) : L'aire du domaine délimité par la courbe est supérieure à 1,
c) : la fonction est dérivable donc continue,
d) : la fonction courbe n'admet qu'une seule tangente « horizontale ».
2. Sur l'intervalle , on a :
| a) | b) | c) | d) |
La tangente à au point d'abscisse 0 est « horizontale », donc .
La bonne réponse est la réponse c.
3. On admet qu'une équation de la tangente à la courbe au point d'abscisse 4 est :
Le nombre dérivé de en 4 est :
| a) | b) | c) | d) |
Le coefficient directeur de la droite indiquée est .
La bonne réponse est la réponse c.
4. On pose . Un encadrement de est :
| a) | b) | c) | d) |
On évalue l'aire du domaine délimité par , l'axe des abscisses et les droites d'équations et .
La bonne réponse est la réponse c.
