Sujet et corrigé de l'exercice 3 du bac ES de maths de mai 2014 en Amérique du nord
Cacher les corrigés
Un site est spécialisé dans la diffusion de vidéos sur Internet.
Le responsable du site a constaté que la durée de chargement des vidéos évoluait en fonction du nombre d'internautes connectés simultanément.
On cherche à estimer la durée de chargement en fonction du nombre de personnes connectées simultanément.
Deux fonctions sont proposées pour modéliser cette situation.
Partie A : Modèle exponentiel
Dans le repère orthogonal ci-dessous, on a tracé la courbe représentative d'un fonction qui modélise la situation précédente.
On note le nombre, exprimé en millier, d'internautes connectés simultanément et la durée du chargement exprimé en seconde.
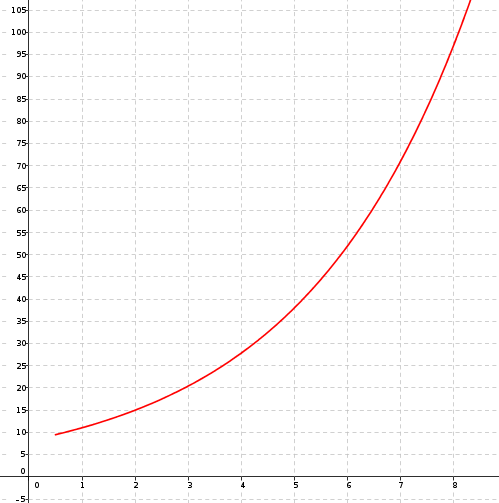
1. Par lecture graphique, estimer la durée de chargement, en seconde, pour 8 000 personnes connectées.
On lit l'image de 8 par la fonction : 96.
Donc on peut estimer la durée de chargement autour de 96 secondes.
2.a. Déterminer graphiquement un antécédent de 15 par .
Un antécédent de 15 est 2.
b. Donner une interprétation de ce résultat.
Si le temps de chargement est de 15 secondes alors il y a 2 000 personnes connectées.
Partie B : Modèle logarithmique
On considère une autre fonction pour modéliser la situation précédente.
On note le nombre, exprimé en millier, d'internautes connectés simultanément.
La durée de chargement en seconde est alors avec pour :
1.a. Calculer
La fonction est dérivable sur et on a directement :
b. Dresser le tableau de variation de sur l'intervalle
On étudie le signe de , pour tout :
De même : et
On a donc le tableau de variations :
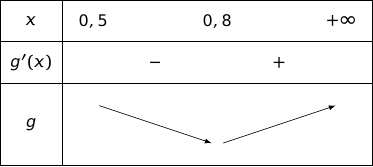
2.a. Justifier que la fonction définie sur par :
est une primitive de sur .
La fonction est dérivable sur et on a :
avec :
;
;
Du coup :
Donc est bien une primitive de sur .
b. On pose
Montrer que la valeur exacte de I peut s'écrire sous la forme où et sont deux entiers relatifs que l'on déterminera.
c. Déterminer une valeur approchée à près de I puis donner une interprétation de ce résultat.
On a .
L'intégrale calculée est la valeur moyenne de la fonction sur .
Pour un nombre de 2 000 à 4 000 connectés simultanément, le temps moyen de téléchargement est de 21 secondes 36 centièmes.
Partie C
Une vidéo particulièrement demandée a attiré simultanément 8 000 personnes.
On a constaté que le temps de chargement était de 92 secondes.
Déterminer, en justifiant, celui des deux modèles qui décrit le mieux la situation pour cette vidéo.
Dans le modèle exponentiel de la partie A on a vu que pour 8 000 connectés simultanément, le temps de chargment était de 96 secondes environ.
Avec le modèle logarithmique ce temps est de :
Donc le modèle qui décrit le mieux la situation est le modèle exponentiel.
