Sujet et corrigé de l'exercice de spécialité du bac ES de maths de mai 2014 en Amérique du nord
Cacher les corrigés
Lors d'une campagne électorale, un homme politique doit effectuer une tournée dans les villes A, B, C, D, E, F, G et H, en utilisant le réseau autoroutier.
Le graphe ci-dessous, représente les différentes villes de la tournée et les tronçons d'autoroute reliant ces villes (une ville est représentée par un sommet, un tronçon d'autoroute par une arête) :
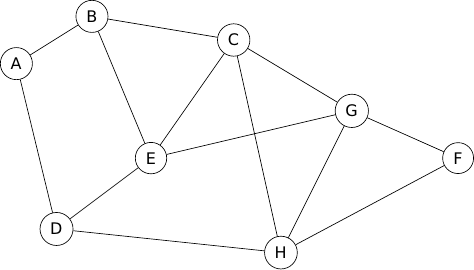
Partie A
1. Déterminer, en justifiant, si le graphe est :
a. complet ;
b. connexe.
Le graphe n'est pas complet, en effet, par exemple, les sommets A et E ne sont pas directement reliés par une arête.
Le graphe est connexe, en effet il existe toujours un chemin permettant de relier deux sommets quelconques du graphe.
2.a. Justifier qu'il est possible d'organiser la tournée en passant au moins une fois par chaque ville, tout en empruntant une fois et une seule chaque tronçon d'autoroute.
Voici le tableau qui donne le degré de chaque sommet :
| A | B | C | D | E | F | G | H |
| 2 | 3 | 4 | 3 | 4 | 2 | 4 | 4 |
On remarque que tous les sommets sont de degré pair sauf les sommets B et D qui sont de degré impair.
Le graphe étant connexe, il existe une chaîne eulérienne permettant de relier les sommets B et D, c'est à dire qu'il est possible d'organiser la tournée en passant au moins une fois par chaque ville, tout en empruntant une fois et une seule chaque tronçon d'autoroute.
b. Citer un trajet de ce type.
B, C, E, B, A, D, H, G, F, H, C, G, E, D
3. On appelle M la matrice d'adjacence associée au graphe (les sommets étant pris dans l'ordre alphabétique).
a. Déterminer la matrice M.
b. On donne la matrice
Déterminer, en justifiant, le nombre de chemins de longueur 3 reliant E à H.
Préciser ces chemins.
Dans la matrice , on lit sur la 5ème ligne, le nombre figurant en dernière position, c'est 4.
Donc il y a 4 chemins distincts de longueur 3 reliant E à H qui sont :
E, C, G, H
E, G, F, H
E, G, C, H
E, B, C, H
Partie B
Des contraintes d'organisation obligent cet homme politique à se rendre dans la ville F après la ville A.
Le graphe est complété ci-dessous par les longueurs en kilomètre de chaque tronçon d'autoroute.
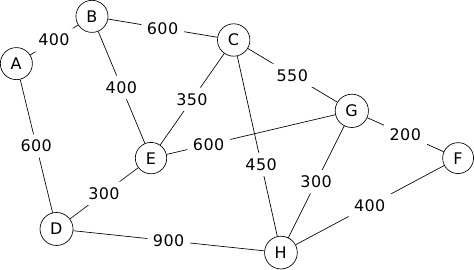
Déterminer, en utilisant l'algorithme de Dijkstra, le trajet autoroutier le plus court pour aller de A à F.
Préciser la longueur en kilomètres de ce trajet.
Voici les étapes de l'algorithme de Dijkstra présentées sous forme de tableau :
| A | B | C | D | E | G | H | F |
| 0 | 400,A | 600,A | |||||
| / | 1000,B | 600,A | 800,B | ||||
| / | / | 1000,B | 900,D | 1500,D | |||
| / | / | 1150,E | / | 1400,E | 1500,D | ||
| / | / | / | / | 1550,C | 1450,C | ||
| / | / | / | / | / | 1700,G | 1600,G | |
| / | / | / | / | / | / | 1850,H | |
| / | / | / | / | / | / | / |
Donc le trajet le plus court est A, B, E, G, F et il fait 1600 km.
