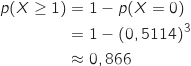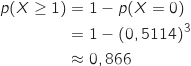Corrigé de l'exercice 2 du bac ES de maths de juin 2012 aux Antilles
Cacher les corrigés
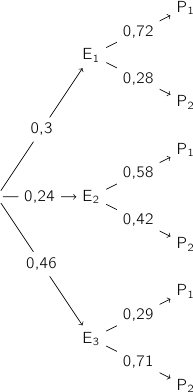
Un restaurant propose une formule « entrée + plat » pour laquelle chaque client choisit entre trois entrées (numérotées 1, 2 et 3) puis entre deux plats (numérotés 1 et 2). Chaque client qui choisit cette formule prend une entrée et un plat. On a constaté que : 30 % des clients choisissent l'entrée 1, 24 % choisissent l'entrée 2 et les autres clients choisissent l'entrée 3. Par ailleurs, le plat 1 est choisi par : 72 % des clients ayant opté pour l'entrée 1, 58 % des clients ayant opté pour l'entrée 2 et 29 % des clients ayant opté pour l'entrée 3. On choisit au hasard un client du restaurant ayant opté pour la formule « entrée + plat ». On note :- E
l'évènement : « Le client choisit l'entrée 1 » ;
- E
l'évènement : « Le client choisit l'entrée 2 » ;
- E
l'évènement : « Le client choisit l'entrée 3 » ;
- P l'évènement : « Le client choisit le plat 1 » ;
- P l'évènement : « Le client choisit le plat 2 ».
1. Traduire la situation étudiée à l'aide d'un arbre pondéré en indiquant sur cet arbre les probabilités données dans l'énoncé.
2. Quelle est la probabilité que le client choisisse l'entrée 3 et le plat 1 (on donnera la valeur exacte de cette probabilité) ?
On calculer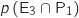 
en utilisant le principe multiplicatif sur l'arbre :
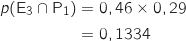
3. Montrer que la probabilité de l'évènement P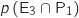 en utilisant le principe multiplicatif sur l'arbre :
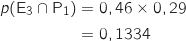
est égale à 0,4886.
Les événements E, E et E forment une partition de l'univers donc d'après la formule des probabilités totales on a :
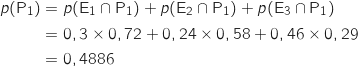
4. Quelle est la probabilité qu'un client ait choisi l'entrée 1 sachant qu'il a pris le plat 1 (on arrondira le résultat à , E et E forment une partition de l'univers donc d'après la formule des probabilités totales on a :
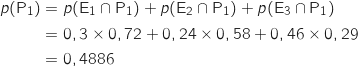
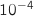près) ?
On calcule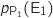 
avec la formule :
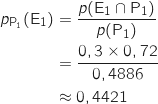
5. On choisit trois clients au hasard parmi ceux ayant opté pour la formule ;
on suppose le nombre de clients suffisament grand pour assimiler ce choix à des tirages successifs avec remise.
Dans cette question, on arrondira les résultats au millième.
a. Déterminer la probabilité qu'exactement deux de ces clients aient pris le plat 1.
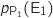avec la formule :
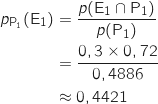
On considère l'expérience de Bernoulli associée à la situation dont la loi est donnée par :
On répète cette expérience 3 fois de suite et de manière indépendante. La variable aléatoire 
qui
compte le nombre de clients qui ont choisit le plat 1 suit une loi binomiale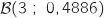 
.
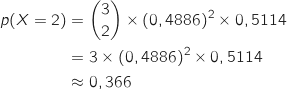
b. Déterminer la probabilité qu'au moins un client ait pris le plat 1.
qui
compte le nombre de clients qui ont choisit le plat 1 suit une loi binomiale .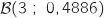
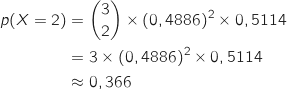
Il s'agit de calculer :
