Corrigé de l'exercice 3 du bac ES de maths de juin 2012 aux Antilles
Cacher les corrigés
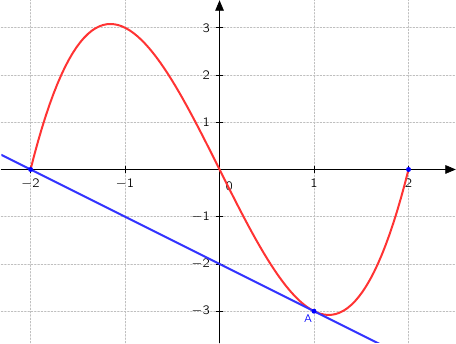
On donne la courbe représentative d'une fonction
définie et dérivable sur l'intervalle 
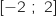, et sa tangente en son point A d'abscisse 1 ;
cette tangente passe par le point de coordonnées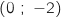 
. On note 
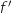la fonction dérivée de sur l'intervalle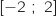 
.
1. Le nombre dérivé noté
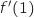est égal à :
Le nombre dérivé au point d'abscisse 1 est le coefficient directeur de la tangente à la courbe en ce point, c'est à dire le coefficient directeur de la tangente
en A.
Par lecture graphique on a :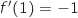 
.
La bonne réponse est c).
2. La fonction .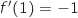
La bonne réponse est c).
telle que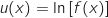 
est définie sur :
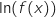est définie si et seulement si 
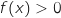car la fonction 
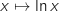est définie sur 
.
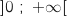Sur le graphique 
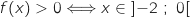, donc est définie sur cet intervalle.
La bonne réponse est b).
3. On considère
une primitive de sur l'intervalle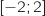 
.
La fonction est décroissante sur :
Si est une primitive de alors pour tout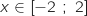 
; 
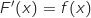et donc le signe de permet de déterminer les variations de .
En particulier est décroissante sur l'intervalle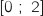 
où est négative.
La bonne réponse est c).
4. Soit est une primitive de alors pour tout 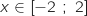; 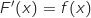et donc le signe de permet de déterminer les variations de .
En particulier est décroissante sur l'intervalle 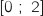où est négative.
La bonne réponse est c).
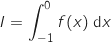. On a :
Sur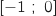 
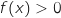; et par observation du graphique l'aire délimitée par la courbe de ; la droite
d'équation 
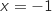et les axes du repère est comprise entre 1 et 3. L'intégrale 
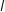représente cette aire, donc 
.
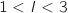La bonne réponse est c).
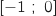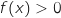; et par observation du graphique l'aire délimitée par la courbe de ; la droite
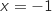d'équation et les axes du repère est comprise entre 1 et 3. L'intégrale 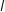représente cette aire, donc .
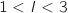La bonne réponse est c).
