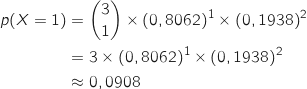Corrigé de l'exercice 3 du bac ES de maths de juin 2012 en Asie
Cacher les corrigés
L'opérateur téléphonique Boomtel propose à ses abonnés deux types d'accès internet à haut débit :- un accès internet sur ligne fixe ;
- un accès 3G sur téléphone portable.
- 58 % des abonnés ont un accès internet sur ligne fixe. Parmi ceux-là, 24 % ont également un accès 3G sur téléphone portable ;
- parmi les abonnés qui n'ont pas d'accès internet sur ligne fixe, 13 % ont un accès 3G sur téléphone portable.
- la probabilité de l'évènement A est notée
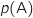 ;
;
- si
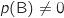 ,
, 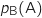 désigne la probabilité de l'évènement A sachant que l'évènement B est réalisé ;
désigne la probabilité de l'évènement A sachant que l'évènement B est réalisé ;
- l'évènement contraire de l'évènement A est noté
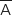 .
.
Pour une enquête de satisfaction, la fiche d'un abonné est prélevée au hasard. Dans cet exercice on note :
- F l'évènement : « la fiche est celle d'un abonné qui a un accès internet sur ligne fixe » ;
- G l'évènement : « la fiche est celle d'un abonné qui a un accès 3G sur téléphone portable ».
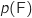 , de
, de 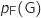 et de
et de 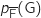 .
.
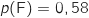 (58 % des abonnés ont un accès sur ligne fixe).
(58 % des abonnés ont un accès sur ligne fixe).
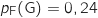 (parmi ceux-là 24 % ont également un accès 3G).
(parmi ceux-là 24 % ont également un accès 3G).
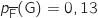 (parmi les abonnés qui n'ont pas d'accès internet sur ligne fixe, 13 % ont un accès 3G).
(parmi les abonnés qui n'ont pas d'accès internet sur ligne fixe, 13 % ont un accès 3G).
3. Calculer
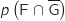 .
Interpréter ce résultat.
.
Interpréter ce résultat.
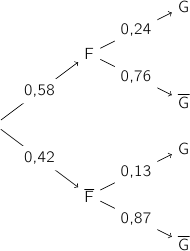
En utilisant le principe multiplicatif sur les branches de l'arbre on a :
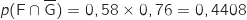 Ainsi, 44,08 % des abonnés ont uniquement un accès internet sur ligne fixe (et pas d'accès 3G).
Ainsi, 44,08 % des abonnés ont uniquement un accès internet sur ligne fixe (et pas d'accès 3G).
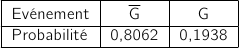
4.a. Vérifier que la probabilité que la fiche prélevée soit celle d'un abonné qui n'a pas d'accès 3G sur téléphone portable est de 0,8062.
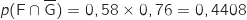 Ainsi, 44,08 % des abonnés ont uniquement un accès internet sur ligne fixe (et pas d'accès 3G).
Ainsi, 44,08 % des abonnés ont uniquement un accès internet sur ligne fixe (et pas d'accès 3G).
Les événements F et 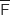 forment une partition de l'univers. Donc d'après la formule des probabilités totales :
forment une partition de l'univers. Donc d'après la formule des probabilités totales :

b. Peut-on affirmer qu'au moins 25 % des abonnés ont un accès 3G sur téléphone portable ?
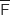 forment une partition de l'univers. Donc d'après la formule des probabilités totales :
forment une partition de l'univers. Donc d'après la formule des probabilités totales :

D'après la question précédente environ 80 % des abonnés n'ont pas d'accès 3G. Donc il y a environ 20 % des abonnés seulement qui ont un accès 3G.
On ne peut pas faire l'affirmation proposée.
5. On prélève successivement les fiches de trois abonnés. On admet que le nombre de fiches est suffisamment grand pour qu'on puisse assimiler le tirage à un tirage avec remise.
Calculer la probabilité qu'exactement une des fiches tirées soit celle d'un abonné qui n'a pas d'accès 3G sur téléphone portable.
L'expérience de Bernoulli associée à la situation proposée a les deux issues 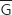 (succès) et G (échec) et on a la loi :
(succès) et G (échec) et on a la loi :
On répète 3 fois cette expérience de façon indépendante ; donc la variable aléatoire  qui compte le nombre de succès (
qui compte le nombre de succès (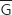 ) suit une loi
binomiale
) suit une loi
binomiale 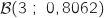 et on a :
et on a :
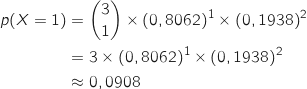
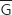 (succès) et G (échec) et on a la loi :
(succès) et G (échec) et on a la loi :

 qui compte le nombre de succès (
qui compte le nombre de succès (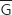 ) suit une loi
binomiale
) suit une loi
binomiale 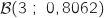 et on a :
et on a :