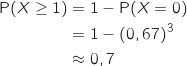Corrigé de l'exercice 3 du bac ES de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
Un sondage a été effectué auprès des anciens élèves d'un lycée quelques années après l'obtention de leur baccalauréat. Ce sondage révèle que 55% d'entre eux poursuivent leurs études à la faculté, 10% ont intégré une école d'ingénieur et le pourcentage restant est sur le marché du travail (en activité ou en recherche d'emploi). Ce sondage révèle aussi que :- 45 % des anciens élèves qui poursuivent leurs études à la faculté ont fait le choix de vivre en colocation ;
- 30 % des anciens élèves qui ont intégré une école d'ingénieur ont fait le choix de vivre en colocation ;
- 15 % des anciens élèves sur le marché du travail ont fait le choix de vivre en colocation.
- F l'évènement : « l'ancien élève poursuit ses études à la faculté » ;
- I l'évènement : « l'ancien élève a intégré une école d'ingénieur » ;
- T l'évènement : « l'ancien élève est sur le marché du travail » ;
- C l'évènement : « l'ancien élève vit en colocation ».
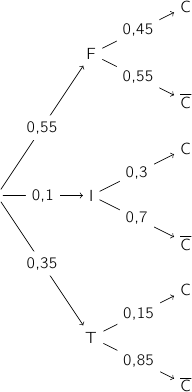
1) Construire un arbre pondéré décrivant la situation.
2)a) Exprimer à l'aide d'une phrase l'évènement
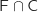 puis calculer la valeur exacte de sa probabilité.
puis calculer la valeur exacte de sa probabilité.
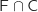 : « L'ancien élève suit des études à la faculté et est en colocation ».
En utilisant le principe multiplicatif sur l'arbre on a :
: « L'ancien élève suit des études à la faculté et est en colocation ».
En utilisant le principe multiplicatif sur l'arbre on a :
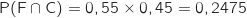
Les événements F, I et T forment une partition de l'univers ; donc d'après la formule des probabilités totales :
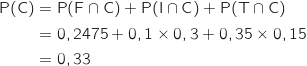
3) Un ancien élève vit en colocation. Calculer la probabilité qu'il poursuive ses études à la faculté.
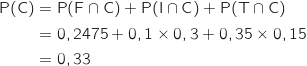
Il s'agit de calculer 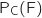 et on a :
et on a :
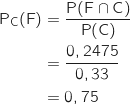
4) Dans cette question, toute trace de recherche, même incomplète, ou d'initiative même non fructueuse, sera prise en compte dans l'évaluation.
Le responsable du sondage affirme : « Plus de la moitié des élèves n'ayant pas fait le choix de la colocation poursuivent des études ».
Cette affirmation est-elle correcte ? Justifier.
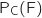 et on a :
et on a :
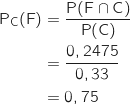
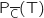 donne la proportion des anciens élèves qui travaillent parmi ceux qui ne sont pas en colocation et on a :
donne la proportion des anciens élèves qui travaillent parmi ceux qui ne sont pas en colocation et on a :
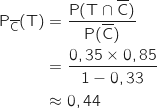 Donc environ 44 % des anciens élèves n'ayant pas fait le choix de la colocation travaillent donc plus de la moitié font des études. L'affirmation est vraie.
Donc environ 44 % des anciens élèves n'ayant pas fait le choix de la colocation travaillent donc plus de la moitié font des études. L'affirmation est vraie.
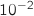 près.
près.
On répète 3 fois de façon indépendante l'expérience de Bernoulli dont la loi est donnée par :
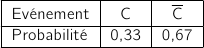
La variable aléatoire  qui compte le nombre de fois où on obtient l'événement C suit une loi binomiale
qui compte le nombre de fois où on obtient l'événement C suit une loi binomiale 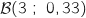 .
On cherche :
.
On cherche : 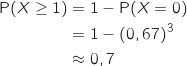

 qui compte le nombre de fois où on obtient l'événement C suit une loi binomiale
qui compte le nombre de fois où on obtient l'événement C suit une loi binomiale 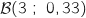 .
On cherche :
.
On cherche :