Corrigé de l'exercice 4 du bac ES de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
PARTIE A
Soit la fonction définie sur
la fonction définie sur  par
par 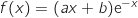 où
où  et
et  sont deux réels.
On note
sont deux réels.
On note 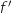 la fonction dérivée de
la fonction dérivée de  .
1. Montrer que pour tout nombre réel
.
1. Montrer que pour tout nombre réel  ,
, 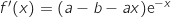 .
.
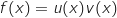 avec :
avec :
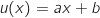
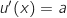
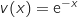
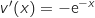 Donc
Donc 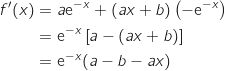
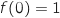 et
et 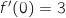 . En déduire
. En déduire  et
et  .
.
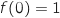 , donc
, donc 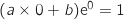 , soit
, soit 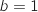 .
.
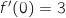 , donc
, donc 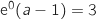 soit
soit 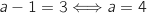 .
.
PARTIE B
Dans cette partie, on admettra que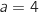 et
et 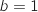 .
Donc pour tout réel
.
Donc pour tout réel  ,
, 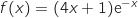 .
.
Les questions 1 et 2 du sujet original portent sur la notion de limite. Cette notion ne fait plus partie des programmes.
3. Etudier le sens de variation de  sur
sur  .
.
En utilisant la formule de la dérivée trouvée dans la partie A on a :
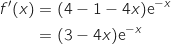 Pour tout
Pour tout  ,
, 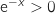 , du coup le signe de la dérivée est le même que celui de
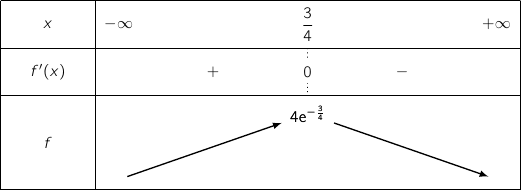
, du coup le signe de la dérivée est le même que celui de 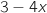 et on a le tableau de variations :
et on a le tableau de variations :
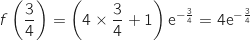 .
.
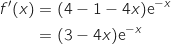 Pour tout
Pour tout  ,
, 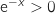 , du coup le signe de la dérivée est le même que celui de
, du coup le signe de la dérivée est le même que celui de 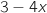 et on a le tableau de variations :
et on a le tableau de variations :

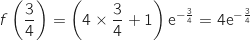 .
.
PARTIE C
Une entreprise produit centaines d'objets chaque semaine.
Le coût de production, exprimé en milliers d'euros, est défini sur l'intervalle
centaines d'objets chaque semaine.
Le coût de production, exprimé en milliers d'euros, est défini sur l'intervalle 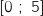 par la fonction
par la fonction  étudiée dans la partie B.
1. Quel est le coût de production maximal hebdomadaire ? On arrondira le résultat à l'euro près.
étudiée dans la partie B.
1. Quel est le coût de production maximal hebdomadaire ? On arrondira le résultat à l'euro près.
D'après l'étude de la fonction vue dans la partie A, le coût de production maximal est
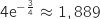 milliers d'euros soit environ 1889 euros.
milliers d'euros soit environ 1889 euros.
2. Démontrer que la fonction 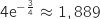 milliers d'euros soit environ 1889 euros.
milliers d'euros soit environ 1889 euros.
 définie sur
définie sur 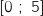 par
par 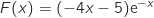 est une primitive de la fonction
est une primitive de la fonction  sur ce même intervalle.
sur ce même intervalle.
Pour vérifier que  est une primitive de
est une primitive de  on calcule
on calcule 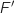 .
.
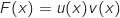 avec :
avec :
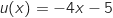
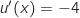
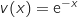
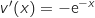
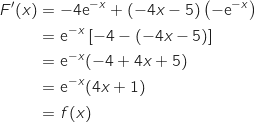 Donc
Donc  est bien une primitive de
est bien une primitive de  .
.
3.a. Calculer  est une primitive de
est une primitive de  on calcule
on calcule 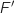 .
.
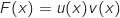 avec :
avec :
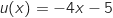
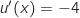
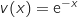
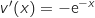
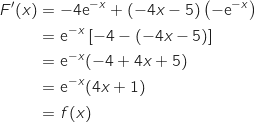 Donc
Donc  est bien une primitive de
est bien une primitive de  .
.
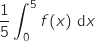 . On arrondira le résultat à
. On arrondira le résultat à 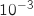 près.
près.
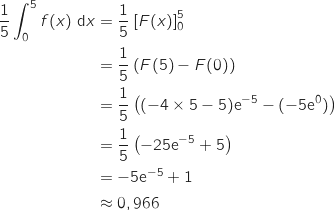
Le calcul précédent correspond à la valeur moyenne de  sur
sur 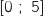 .
Donc on peut dire qu'en moyenne le coût de production hebdomadaire est d'environ 966 euros.
.
Donc on peut dire qu'en moyenne le coût de production hebdomadaire est d'environ 966 euros.
 sur
sur 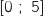 .
Donc on peut dire qu'en moyenne le coût de production hebdomadaire est d'environ 966 euros.
.
Donc on peut dire qu'en moyenne le coût de production hebdomadaire est d'environ 966 euros.
