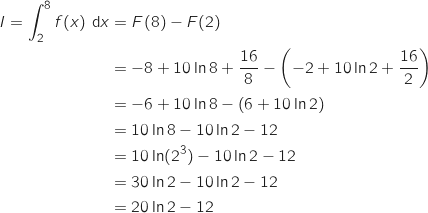Sujet et corrigé de l'exercice 3 du bac ES de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
On considère la fonction définie sur l'intervalle
définie sur l'intervalle 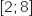 par :
par :
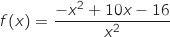
On appelle
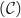 sa courbe représentative dans un repère.
1. Montrer que pour tout réel de l'intervalle
sa courbe représentative dans un repère.
1. Montrer que pour tout réel de l'intervalle 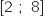 , on a :
, on a :
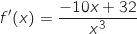
La fonction proposée est dérivable sur 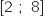 et se présente sous la forme
et se présente sous la forme
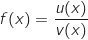 avec :
avec :
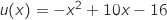 ;
; 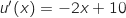
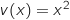 ;
; 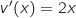 Donc :
Donc : 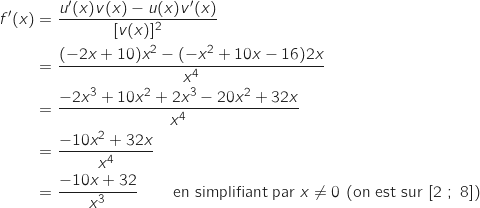
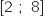 et se présente sous la forme
et se présente sous la forme
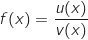 avec :
avec :
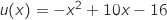 ;
; 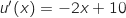
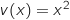 ;
; 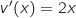 Donc :
Donc : 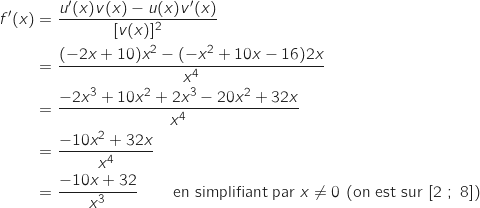
2.a. Etudier le signe de
 sur l'intervalle
sur l'intervalle 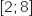 .
.
Pour tout 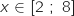 ,
, 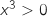 , donc le signe de
, donc le signe de  est le même que celui
de
est le même que celui
de 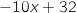 .
Le binome
.
Le binome 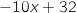 s'annule pour
s'annule pour 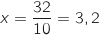 et comme le coefficient
de
et comme le coefficient
de  est négatif il est positif pour
est négatif il est positif pour 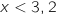 et négatif pour
et négatif pour 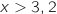 .
.
b. En déduire le tableau de variations de 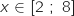 ,
, 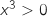 , donc le signe de
, donc le signe de  est le même que celui
de
est le même que celui
de 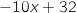 .
Le binome
.
Le binome 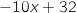 s'annule pour
s'annule pour 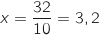 et comme le coefficient
de
et comme le coefficient
de  est négatif il est positif pour
est négatif il est positif pour 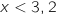 et négatif pour
et négatif pour 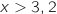 .
.
 sur l'intervalle
sur l'intervalle 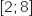 .
.
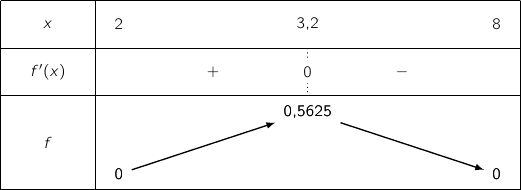
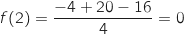
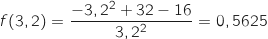
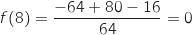
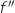 la dérivée seconde de
la dérivée seconde de  sur
sur 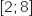 .
On admet que, pour tout réel
.
On admet que, pour tout réel  de l'intervalle
de l'intervalle 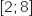 , on a :
, on a :
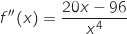
 est une fonction convexe sur
est une fonction convexe sur 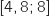 .
.
Pour tout 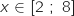 ,
, 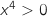 , donc le signe de
, donc le signe de 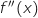 est le même que celui
de
est le même que celui
de 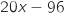 .
C'est encore un binôme du premier degré, qui cette fois s'annule pour
.
C'est encore un binôme du premier degré, qui cette fois s'annule pour 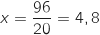 .
On a donc le signe de
.
On a donc le signe de 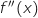 :
:

Pour tout 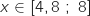 ,
, 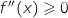 , donc
, donc  est convexe sur cet intervalle.
est convexe sur cet intervalle.
b. Montrer que le point de 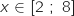 ,
, 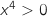 , donc le signe de
, donc le signe de 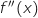 est le même que celui
de
est le même que celui
de 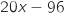 .
C'est encore un binôme du premier degré, qui cette fois s'annule pour
.
C'est encore un binôme du premier degré, qui cette fois s'annule pour 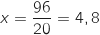 .
On a donc le signe de
.
On a donc le signe de 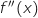 :
:

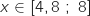 ,
, 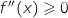 , donc
, donc  est convexe sur cet intervalle.
est convexe sur cet intervalle.
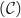 d'abscisse
d'abscisse 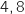 est un point d'inflexion.
est un point d'inflexion.
D'après l'étude de signe précédente 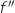 s'annule en changeant de signe en
s'annule en changeant de signe en 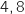 , donc
la courbe
, donc
la courbe 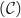 a un point d'inflexion au point d'abscisse 4,8.
a un point d'inflexion au point d'abscisse 4,8.
4. On considère la fonction 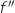 s'annule en changeant de signe en
s'annule en changeant de signe en 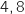 , donc
la courbe
, donc
la courbe 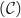 a un point d'inflexion au point d'abscisse 4,8.
a un point d'inflexion au point d'abscisse 4,8.
 définie sur
définie sur 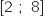 par :
par :
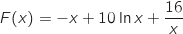
 est une primitive de
est une primitive de  sur
sur 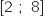 .
.
La fonction  proposée est dérivable sur
proposée est dérivable sur 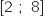 et on a :
et on a :
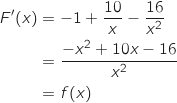 Cela prouve que
Cela prouve que  est une primitive de
est une primitive de  sur l'intervalle considéré.
sur l'intervalle considéré.
b. Calculer  proposée est dérivable sur
proposée est dérivable sur 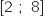 et on a :
et on a :
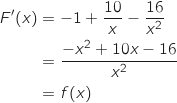 Cela prouve que
Cela prouve que  est une primitive de
est une primitive de  sur l'intervalle considéré.
sur l'intervalle considéré.