Sujet et corrigé de l'exercice de spécialité du bac ES de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
Dans le graphe ci-dessous, les sommets représentent différentes zones de résidence ou d'activités d'une municipalité. Une arête reliant deux de ces sommets indique l'existence d'une voie d'accès principale entre deux lieux correspondants.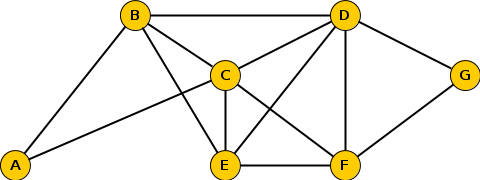
1. Donner, sans justifier, le degré de chacun des sommets (la réponse pourra être présentée sous forme de tableau où les sommets seront mis dans l'ordre alphabétique).
On obtient :
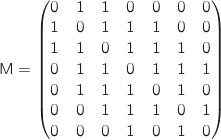
b. On donne la matric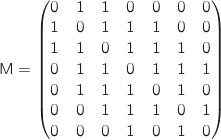e 
Déterminer, en justifiant, le nombre de chemins de longueur 3 reliant A et F puis donner leur liste.
On lit dans la matrice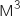 
le coefficient à la première ligne (A) et à la 6
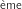colonne (F). On trouve 5. Donc il y a 5 chemins de longueur 3 reliant A à F.
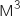le coefficient à la première ligne (A) et à la 6
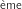colonne (F). On trouve 5. Donc il y a 5 chemins de longueur 3 reliant A à F.
- A, B, C, F
- A, B, D, F
- A, B, E, F
- A, C, E, F
- A, C, D, F
3. Pour sa campagne électorale, un candidat souhaite parcourir toutes les voies d'accès principales de ce quartier sans emprunter plusieurs fois la même voie. Montrer qu'un tel parcours est possible.
En observant le tableau des degrés des sommets (question 1) on remarque que le
graphe possède exactement deux sommets de degrés impairs : C et D.
Ce graphe est connexe, donc il admet une chaine eulérienne d'extrémités C et D.
Le parcours envisagé par le candidat est donc possible.
4. Dans le graphe ci-dessous, les valeurs indiquent, en minutes, les durées moyennes des trajets entre les différents lieux via les transports en commun.
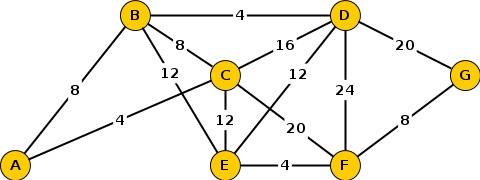
On présente l'algorithme sous la forme usuelle de tableau :
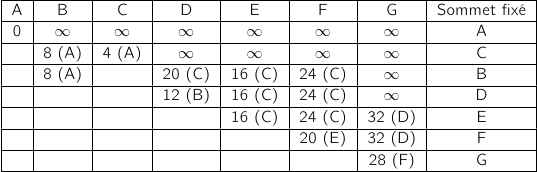
Le chemin de durée minimale est donc : A, C, E, F, G.
b. Combien de temps faut-il prévoir pour effectuer ce trajet ?
D'après la question précédente le temps de trajet est de 28 minutes.
