Sujet et corrigé de l'exercice 1 du bac ES de maths de juin 2014 dans les centres étrangers
Cacher les corrigés
Une grande entreprise vient de clôturer sa campagne de recrutement qui s'est déroulée en deux temps :
premier temps : étude du dossier présenté par le candidat ;
deuxième temps : entretien en vue du recrutement.
Le processus de recrutement mis en oeuvre par l'entreprise est le suivant :
si le dossier est jugé de bonne qualité, alors le candidat est reçu en entretien par le directeur des ressources humaines ;
si le dossier n'est pas jugé de bonne qualité, alors le candidat subit des tests puis est reçu en entretien par le directeur de l'entreprise.
Dans les deux cas, à l'issue de l'entretien, le candidat est recruté ou ne l'est pas.
A l'issue de cette campagne de recrutement, l'entreprise publie les résultats suivants :
30 % des candidats avaient un dossier jugé de bonne qualité ;
20 % des candidats n'ayant pas un dossier jugé de bonne qualité ont été recrutés ;
38 % des candidats ont été recrutés.
1. On prend un candidat au hasard et on note :
D l'événement « le candidat a un dossier jugé de bonne qualité » ;
R l'événement « le candidat est recruté par l'entreprise ».
a. Réprésenter cette situation à l'aide d'un arbre pondéré.
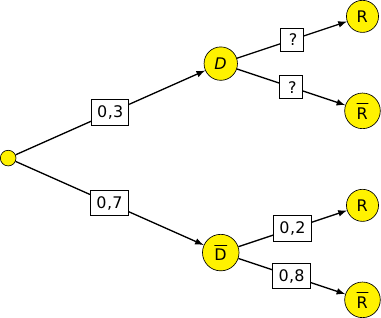
b. Calculer la probabilité que le candidat n'ait pas un dossier de bonne qualité et ne soit pas recruté par l'entreprise.
En utilisant la formule des probabilités composées :
c. Montrer que la probabilité de l'événement est égale à 0,24.
Les événements D et forment une partition de l'univers.
D'après la formule des probabilités totales :
.
On sait que 38 % des candidats sont recrutés, et en utilisant l'arbre :
.
En remplaçant il vient :
donc :
d. En déduire la probabilité qu'un candidat soit recruté sachant que son dossier est jugé de bonne qualité.
Compléter l'arbre pondéré réalisé dans la question a.
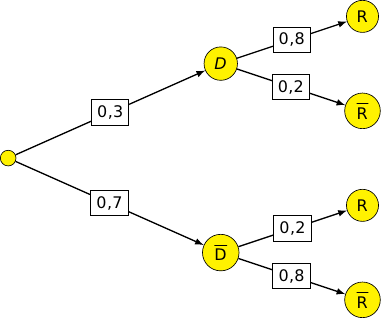
2. Dix personnes postulent pour un emploi dans l'entreprise.
Les études de leurs candidatures sont faites indépendamment les unes des autre.
On désigne par la variable aléatoire donnant le nombre de personnes recrutées parmi les 10 personnes.
a. Justifier que suit une loi binomiale de paramètres et .
On répète 10 fois de façon indépendante une expérience de Bernoulli dont la probabilité du succès (la personne est recrutée) est .
Donc la variable aléatoire qui compte le nombre de succès suit la loi binomiale de paramètre et .
b. Calculer la probabilité qu'au moins une des dix personnes soit recrutée.
On donnera la valeur exacte puis une valeur du résultat arrondie à .
Il est plus facile de calculer la probabilité de l'événement contraire : « Aucune personne n'est recrutée ».
Donc la probabilité demandée est soit .
3. Deux amis, Aymeric et Coralie, sont convoqués le même jour pour un entretien avec la direction des ressources humaines.
Coralie arrive à 8h30 alors qu'Aymeric arrive au hasard entre 8h et 9h.
On désigne par la variable aléatoire donnant l'heure d'arrivée d'Aymeric et on admet que suit la loi uniforme sur l'intervalle .
Déterminer la probabilité pour que Coralie attende Aymeric plus de dix minutes.
Coralie attend Aymeric plus de 10 minutes si celui-ci arrive après 8h40.
La fonction de densité de la loi uniforme sur est la fonction .
On a donc le calcul :
.
