Sujet et corrigé de l'exercice 2 du bac ES de maths de juin 2014 dans les centres étrangers
Cacher les corrigés
Partie A : Etude d'une fonction
Soit la fonction définie sur par :
est la courbe représentative de la fonction dans un repère orthonormé du plan.
On note la fonction dérivée de et la fonction dérivée seconde de .
1.a. Montrer que pour tout réel ,
La fonction est dérivable sur et on peut écrire :
avec :
;
;
Donc :
b. En déduire le sens de variation de sur .
Pour tout réel :
et
Donc pour tout , , ce qui entraîne que la fonction est strictement croissante sur .
2. On admet que pour tout réel ,
Déterminer, en justifiant, l'intervalle sur lequel la fonction est convexe.
Pour tout réel :
et
Donc le signe de est le même que celui de et du coup :
, donc est convexe sur .
3. Soit la fonction définie sur par :
a. Justifier que l'inéquation a pour ensemble de solutions l'intervalle .
L'expression du second degré est négative entre ses racines -1 et 1 et positive à l'extérieur donc l'ensemble des solutions de l'inéquation initiale est .
b. Déterminer le signe de sur l'intervalle .
Pour tout , d'après la question précédente, donc le signe de est le même que celui de , ce qui donne le tableau :

c. En remarquant que pour tout réel , on a l'égalité , déduire de la question précédente la position relative de la courbe et de la droite d'équation sur l'intervalle .
Pour tout réel :
On vient de voir que pour tout :
soit ou encore .
Donc est en dessous de la droite .
4. Soit la fonction définie sur par :
Soit .
On admet que est une primitive de la fonction sur .
Calculer la valeur exacte de .
Partie B : Applications
Sur le graphique suivant, sont tracées sur l'intervalle :
la courbe représentative de la fonction étudiée en partie A ;
la courbe représentative de la fonction définie par ;
la droite d'équation .
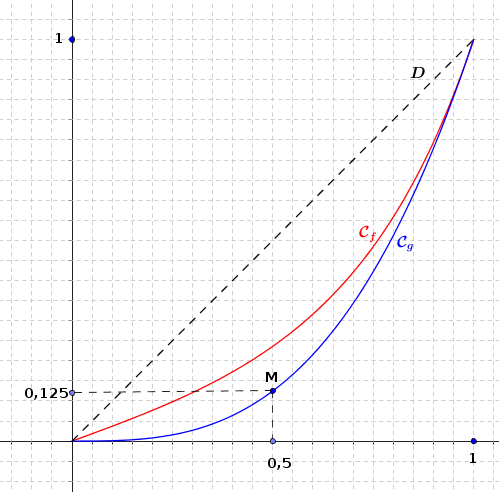
Les courbes et illustrent ici la répartition des salaires dans deux entreprises F et G :
sur l'axe des abscisses, représente la proportion des employés ayant les salaires les plus faibles par rapport à l'effectif total de l'entreprise ;
sur l'axe des ordonnées, et représentent pour chaque entreprise la proportion de la masse salariale (c'est à dire la somme de tous les salaires) correspondante.
Par exemple :
La point M est un point appartenant à la courbe .
Pour l'entreprise G cela se traduit de la façon suivante :
si on classe les employés par revenu croissant, le total des salaires de la première moitié (c'est à dire des 50 % aux revenus les plus faibles) représente 12,5 % de la masse salariale.
1. Calculer le pourcentage de la masse salariale détenue par 80 % des employés ayant les salaires les plus faibles dans l'entreprise F.
On donnera une valeur du résultat arrondie à l'unité.
On calcule :
Donc la proportion de la masse salariale détenue par 80 % des employés ayant les salaires les plus faibles est d'environ 56 %.
2. On note l'aire du domaine délimité par la droite , la courbe et les droites d'équations et .
On appelle indice de Gini associé à la fonction , le nombre réel noté et défini par .
a. Montrer que .
On sait d'après l'étude faite dans la partie A que est en dessous de , donc s'obtient en calculant :
.
Du coup .
b. On admet que, plus l'indice de Gini est petit, plus la répartition des salaires dans l'entreprise est égalitaire.
Déterminer, en justifiant, l'entreprise pour laquelle la distribution des salaires est la plus égalitaire.
On calcule l'indice de Gini pour l'entreprise G.
On remarque déjà que pour , , donc l'aire du domaine utilisé pour le calcul de l'indice de Gini s'obtient par :
Du coup .
Donc c'est l'entreprise F pour laquelle la distribution des salaires est la plus égalitaire.
