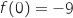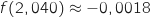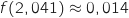Corrigé de l'exercice 2 du bac ES de maths de mai 2012 au Liban
Cacher les corrigés
Partie 1 : Etude d'une fonction
On considère la fonction définie sur
définie sur 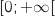 par
par 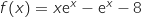 .
1. En écrivant que
.
1. En écrivant que 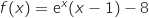 , déterminer la limite de
, déterminer la limite de  en
en  .
.
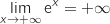 et
et 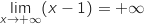 donc
par produit
donc
par produit 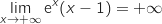 .
Par soustraction de 8, on obtient
.
Par soustraction de 8, on obtient 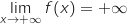 .
.
2. Montrer que
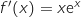 où
où 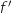 désigne la fonction dérivée de
désigne la fonction dérivée de  sur
sur 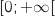 .
.
Pour tout 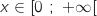 ,
, 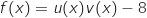 avec :
avec :
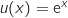
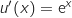
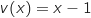
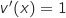 Donc
Donc 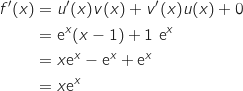
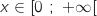 ,
, 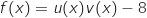 avec :
avec :
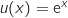
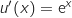
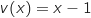
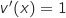 Donc
Donc 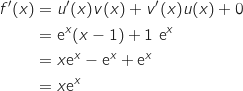
3. Dresser le tableau de variations complet de de
 sur
sur 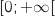 .
.
Pour 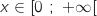 ,
, 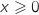 et
et 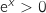 , donc
, donc 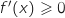 et ne s'annule que pour
et ne s'annule que pour 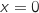 .
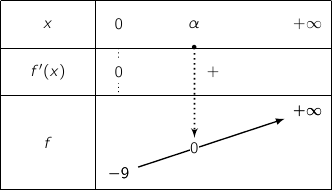
On a alors le tableau de variations :
.
On a alors le tableau de variations :
4.a. Montrer que l'équation 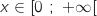 ,
, 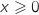 et
et 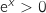 , donc
, donc 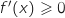 et ne s'annule que pour
et ne s'annule que pour 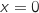 .
On a alors le tableau de variations :
.
On a alors le tableau de variations :

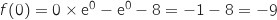
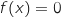 admet sur
admet sur 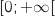 une unique solution
une unique solution  .
.
La fonction  est définie, continue et strictement croissante sur
est définie, continue et strictement croissante sur  avec :
avec :
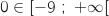 , d'après le théorème des valeurs intermédiaires, l'équation
, d'après le théorème des valeurs intermédiaires, l'équation 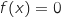 admet une unique solution
admet une unique solution
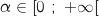 .
.
b. Montrer que  est définie, continue et strictement croissante sur
est définie, continue et strictement croissante sur  avec :
avec :
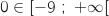 , d'après le théorème des valeurs intermédiaires, l'équation
, d'après le théorème des valeurs intermédiaires, l'équation 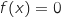 admet une unique solution
admet une unique solution
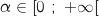 .
.
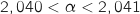 .
.
En utilisant la calculette :
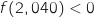 et
et 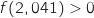 , ce qui entraîne que
, ce qui entraîne que 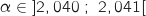 .
.
c. En utilisant les questions précédentes, déduire le signe de 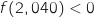 et
et 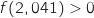 , ce qui entraîne que
, ce qui entraîne que 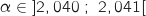 .
.
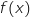 en fonction des valeurs de
en fonction des valeurs de  sur
sur 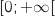 .
.
On a directement le tableau de signes :

5.a. Montrer que la fonction 
 définie sur
définie sur 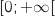 par
par 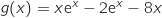 est une primitive de
est une primitive de  sur
sur 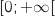 .
.
On calcule la dérivée de la fonction  :
:
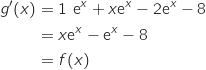 Donc
Donc  est bien une primitive de
est bien une primitive de  sur
sur  .
.
b. Calculer la valeur exacte de  :
:
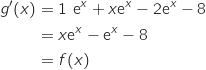 Donc
Donc  est bien une primitive de
est bien une primitive de  sur
sur  .
.
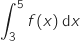 .
.
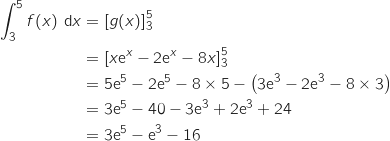
Partie 2 : Application à une situation économique
Une entreprise fabrique milliers d'objets avec
milliers d'objets avec  appartenant à
appartenant à 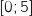 .
La fonction
.
La fonction  de la 1
de la 1 partie modélise les bénéfices ou les pertes de l'entreprise en centaine d'euros.
Pour une quantité
partie modélise les bénéfices ou les pertes de l'entreprise en centaine d'euros.
Pour une quantité  donnée, si
donnée, si 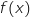 est positif, l'entreprise réalise un bénéfice, et si
est positif, l'entreprise réalise un bénéfice, et si 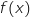 est négatif, l'entreprise subit une perte.
En utilisant les résultats de la 1
est négatif, l'entreprise subit une perte.
En utilisant les résultats de la 1 partie, répondre aux questions suivantes en justifiant :
1. A partir de combien d'objets produits, l'entreprise commence-t-elle à réaliser des bénéfices ?
partie, répondre aux questions suivantes en justifiant :
1. A partir de combien d'objets produits, l'entreprise commence-t-elle à réaliser des bénéfices ?
On a vu que 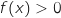 pour
pour 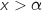 et que
et que 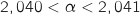 , donc l'entreprise commence à réaliser des bénéfices à partir de 2041 objets.
, donc l'entreprise commence à réaliser des bénéfices à partir de 2041 objets.
2. L'entreprise pense produire régulièrement entre 3 et 5 milliers d'objets.
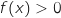 pour
pour 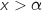 et que
et que 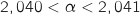 , donc l'entreprise commence à réaliser des bénéfices à partir de 2041 objets.
, donc l'entreprise commence à réaliser des bénéfices à partir de 2041 objets.
Déterminer la valeur moyenne du bénéfice sur
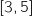 (on donnera le résultat arrondi à l'euro près).
(on donnera le résultat arrondi à l'euro près).
La valeur moyenne du bénéfice sur 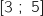 correspond à la valeur moyenne de la fonction
correspond à la valeur moyenne de la fonction  sur
sur 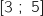 soit :
soit :
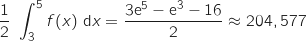 .
Donc la valeur moyenne du bénéfice est d'environ 20458 euros.
.
Donc la valeur moyenne du bénéfice est d'environ 20458 euros.
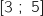 correspond à la valeur moyenne de la fonction
correspond à la valeur moyenne de la fonction  sur
sur 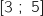 soit :
soit :
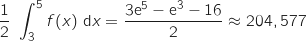 .
Donc la valeur moyenne du bénéfice est d'environ 20458 euros.
.
Donc la valeur moyenne du bénéfice est d'environ 20458 euros.